Work Power and Energy 3 Question 6
6. A $0.5 kg$ block slides from the point $A$ (see fig.) on a horizontal track with an initial speed of $3 m / s$ towards a weightless horizontal spring of length $1 m$ and force constant $2 N / m$. The part $A B$ of the track is frictionless and the part $B C$ has the coefficients of static and kinetic friction as 0.22 and 0.2 respectively. If the distances $A B$ and $B D$ are $2 m$ and $2.14 m$ respectively, find the total distance through which the block moves before it comes to rest completely. (Take $g=10 m / s^{2}$ ).
$(1983,7 M)$
Show Answer
Answer:
Correct Answer: 6. $4.24 m$
Solution:
- From $A$ to $B$, there will be no loss of energy. Now, let block compresses the spring by an amount $x$ and comes momentarily to rest. Then, loss of energy will be equal to the work done against friction. Therefore,
$$ \mu _k m g(B D+x)=\frac{1}{2} m v^{2}-\frac{1}{2} k x^{2} $$
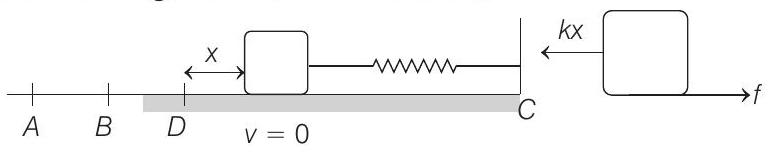
Substituting the values
$$ (0.2)(0.5)(10)(2.14+x)=\frac{1}{2}(0.5)(3)^{2}-\frac{1}{2}(2)(x)^{2} $$
Solving this equation, we get $x=0.1 m$
Now, spring exerts a force $k x=0.2 N$ on the block. But to stop the block from moving limiting static friction is $\mu _s m g=(0.22)(0.5)(10)=1.1 N$. Since, $1.1 N>0.2 N$, block will not move further and it will permanently stop there. Therefore, total distance covered before it comes to rest permanently is
$$ d=A B+B D+x=2+2.14+0.1=4.24 m $$
