Wave Motion 5 Question 14
14. Two loudspeakers $M$ and $N$ are located $20 m$ apart and emit sound at frequencies $118 Hz$ and $121 Hz$, respectively. A car in initially at a point $P, 1800 m$ away from the mid-point $Q$ of the line $M N$ and moves towards $Q$ constantly at $60 km / h$ along the perpendicular bisector of $M N$. It crosses $Q$ and eventually reaches a point $R, 1800 m$ away from $Q$. Let $v(t)$ represent the beat frequency measured by a person sitting in the car at time $t$. Let $v _P, v _Q$ and $v _R$ be the beat frequencies measured at locations $P, Q$ and $R$ respectively. The speed of sound in air is $330 ms^{-1}$. Which of the following statement(s) is (are) true regarding the sound heard by the person?
(2016 Adv.)
(a) The plot below represents schematically the variation of beat frequency with time
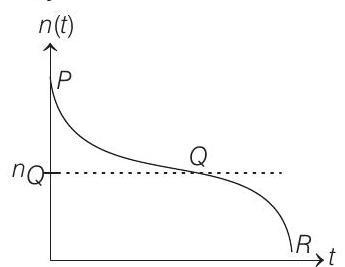
(b) The rate of change in beat frequency is maximum when the car passes through $Q$
(c) $v _P+v _R=2 v _Q$
(d) The plot below represents schematically the variations of beat frequency with time
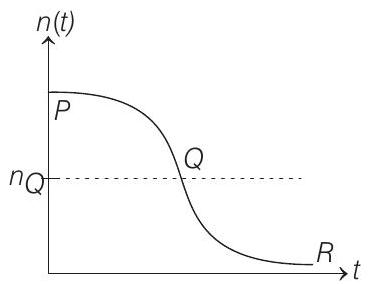
Show Answer
Answer:
Correct Answer: 14. (b, c, d)
Solution:
- Speed of car, $v=60 km / h=\frac{500}{3} m / s$ At a point $S$, between $P$ and $Q$
$$ \begin{aligned} v _M^{\prime} & =v _M\left(\frac{C+v \cos \theta}{C}\right) ; \\ v _N^{\prime} & =v _N\left(\frac{C+v \cos \theta}{C}\right) \\ \Rightarrow \Delta v & =\left(v _n-v _M\right)\left(1+\frac{v \cos \theta}{C}\right) \end{aligned} $$
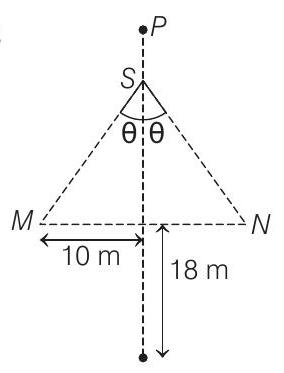
Similarly, between $Q$ and $R$
$$ \begin{aligned} \Delta v & =\left(v _N-v _M\right)\left(1-\frac{v \cos \theta}{C}\right) \\ \frac{d(\Delta v)}{d t} & = \pm\left(v _N-v _M\right) \frac{v}{C} \sin \theta \frac{d \theta}{d t} \end{aligned} $$
$\theta=0^{\circ}$ at the $P$ and $R$ as they are large distance apart.
$\Rightarrow$ Slope of graph is zero.
at $Q, \theta=90^{\circ} \sin \theta$ is maximum also value of $\frac{d \theta}{d t}$ is maximum
as $\frac{d \theta}{d t}=\frac{v}{r}$, where $v$ is its velocity and $r$ is the length of the line joining $P$ and $S$ and $r$ is minimum at $Q$.
$\Rightarrow$ Slope is maximum at $Q$.
At $P, v _P=\Delta v=\left(v _N-v _M\right)\left(1+\frac{v}{C}\right)\left(\theta \approx 0^{\circ}\right)$
At $R, v _R=\Delta v=\left(v _N-v _M\right)\left(1-\frac{v}{C}\right)\left(\theta \approx 0^{\circ}\right)$
At $Q, v _Q=\Delta v=\left(v _N-v _M\right)\left(\theta=90^{\circ}\right)$
From these equations, we can see that
$$ v _P+v _R=2 v _Q $$
