Wave Motion 2 Question 41
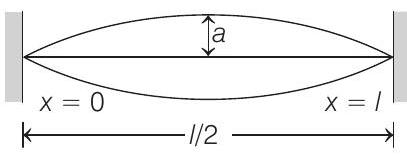
41. A string of mass per unit length
(2003, 4M)
Show Answer
Answer:
Correct Answer: 41.
Solution:
The amplitude at a distance
Total mechanical energy at
or
Here,
Substituting these values in Eq. (i) and integrating it from






