Wave Motion 1 Question 10
10. $Y(x, t)=\frac{0.8}{\left[(4 x+5 t)^{2}+5\right]}$ represents a moving pulse where $x$ and $y$ are in metre and $t$ is in second. Then,
(1999, 3M)
(a) pulse is moving in positive $x$-direction
(b) in $2 s$ it will travel a distance of $2.5 m$
(c) its maximum displacement is $0.16 m$
(d) it is a symmetric pulse
Show Answer
Answer:
Correct Answer: 10. (b, d)
Solution:
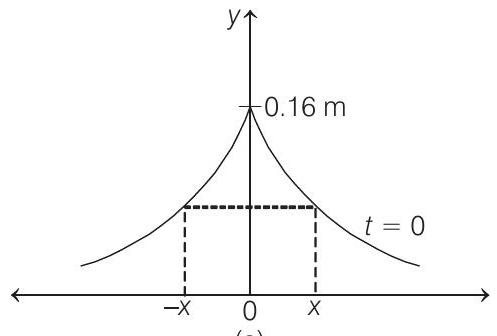
- The shape of pulse at $x=0$ and $t=0$ would be as shown, in Fig. (a).
$$ y(0,0)=\frac{0.8}{5}=0.16 m $$
From the figure it is clear that $y _{\max }=0.16 m$
(a)
Pulse will be symmetric (Symmetry is checked about $y _{\max }$ ) if at $t=0$
$$ y(x)=y(-x) $$
From the given equation,
$$ \begin{aligned} y(x) & =\frac{0.8}{16 x^{2}+5} \\ y(-x) & =\frac{0.8}{16 x^{2}+5} \text { at } t=0 \\ & \text { or } \quad y(x)=y(-x) \end{aligned} $$
Therefore, pulse is symmetric.
Speed of pulse
At $t=1 s$ and $x=-1.25 m$
value of $y$ is again $0.16 m$, i.e. pulse has travelled a distance of $1.25 m$ in $1 s$ in negative $x$-direction or we can say that the speed of pulse is $1.25 m / s$ and it is travelling in negative $x$-direction. Therefore, it will travel a distance of $2.5 m$ in $2 s$.
The above statement can be better understood from Fig. (b).







