Simple Harmonic Motion 5 Question 4
4. A cylindrical plastic bottle of negligible mass is filled with 310 $mL$ of water and left floating in a pond with still water. If pressed downward slightly and released, it starts performing simple harmonic motion at angular frequency $\omega$. If the radius of the bottle is $2.5 cm$, then $\omega$ is close to (Take, density of water $=10^{3} kg / m^{3}$ )
(a) $2.50 rad s^{-1}$
(b) $5.00 rad s^{-1}$
(c) $1.25 rad s^{-1}$
(d) $3.75 rad s^{-1}$
(2019 Main, 10 Jan II)
Show Answer
Answer:
Correct Answer: 4. $(*)$
Solution:
- In equilibrium condition bottle floats in water and its length ’ $l$ ’ inside water is same as the height of water upto which bottle is filled.
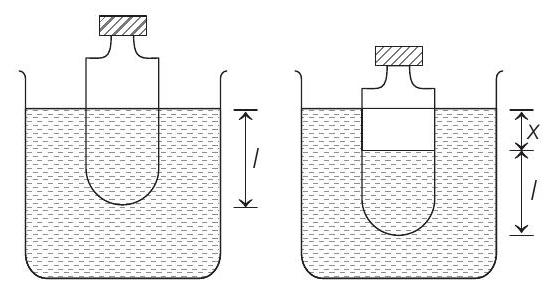
So, $l=$ Volume of water in bottle/Area
$$ =\frac{310}{\pi \times(2.5)^{2}}=15.8 cm=0.158 m $$
When bottle is slightly pushed inside by an amount $x$ then, restoring force acting on the bottle is the upthrust of fluid displaced when bottle goes into liquid by amount $x$.
So, restoring force is;
$$ F=-(\rho A x) g $$
where $\rho=$ density of water,
$A=$ area of cross-section of bottle and
$x=$ displacement from equilibriumposition
But $F=m a$
where, $\quad m=$ mass of water and bottle system
$$ =A l \rho $$
From (i) and (ii) we have,
$$ A l \rho \alpha=-\rho A x g \text { or } a=-\frac{g}{l} x $$
As for SHM, $a=-\omega^{2} x$
We have $\omega=\sqrt{\frac{g}{l}}=\sqrt{\frac{10}{0.158}}=\sqrt{63.29} \approx 8 rad s^{-1}$
$\therefore$ No option is correct.
5 We know that in case of torsonal oscillation frequency
$$ v=\frac{k}{\sqrt{I}} $$
where, $I$ is moment of inertia and $k$ is torsional constant.
$\therefore$ According to question, $v _1=\frac{k}{\sqrt{\frac{M(2 L)^{2}}{12}}}$
(As, MOI of a bar is $I=\frac{M L^{2}}{12}$ )
or
$$ v _1=\frac{k}{\sqrt{\frac{M L^{2}}{3}}} $$
When two masses are attached at ends of rod. Then its moment of inertia is
$$ \frac{M(2 L)^{2}}{12}+2 m \frac{L}{2}^{2} $$
So, new frequency of oscillations is,
$$ \begin{aligned} v _2 & =\frac{k}{\sqrt{\frac{M(2 L)^{2}}{12}+2 m \frac{L^{2}}{2}}} \\ v _2= & \frac{k}{\sqrt{\frac{M L^{2}}{3}+\frac{m L^{2}}{2}}} \end{aligned} $$
As, $\quad v _2=80 %$ of $v _1=0.8 v _1$
So, $\quad \frac{k}{\sqrt{\frac{M L^{2}}{3}+\frac{m L^{2}}{2}}}=\frac{0.8 \times k}{\sqrt{\frac{M L^{2}}{3}}}$
After solving it, we get,
$$ \frac{m}{M}=0.37 $$






