Simple Harmonic Motion 5 Question 20
25. Two non-viscous, incompressible and immiscible liquids of densities $\rho$ and $1.5 \rho$ are poured into the two limbs of a circular tube of radius $R$ and small cross-section kept fixed in a vertical plane as shown in figure. Each liquid occupies one-fourth the circumference of the tube.
$(1991,4+4$ M)
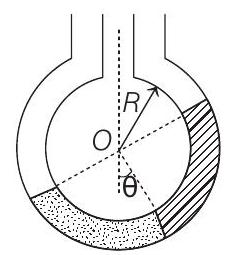
(a) Find the angle $\theta$ that the radius to the interface makes with the vertical in equilibrium position.
(b) If the whole liquid column is given a small displacement from its equilibrium position, show that the resulting oscillations are simple harmonic. Find the time period of these oscillations.
Show Answer
Solution:
- (a) In equilibrium, pressure of same liquid at same level will be same.
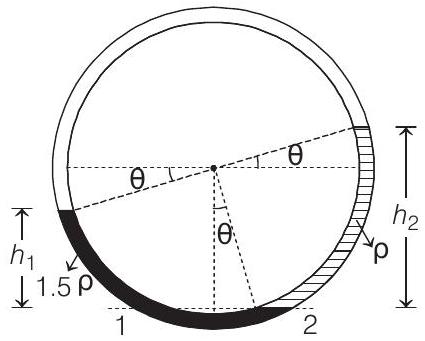
Therefore, $p _1=p _2$ or $p+\left(1.5 \rho g h _1\right)=p+\left(\rho g h _2\right)$ ( $p=$ pressure of gas in empty part of the tube)
$$ \begin{aligned} & \therefore \quad 1.5 h _1=h _2 \\ & 1.5[R \cos \theta-R \sin \theta]=\rho(R \cos \theta+R \sin \theta) \\ & \text { or } \quad 3 \cos \theta-3 \sin \theta=2 \cos \theta+2 \sin \theta \\ & \text { or } \quad 5 \tan \theta=1 \\ & \theta=\tan ^{-1} \frac{1}{5} \end{aligned} $$
(b) When liquids are slightly disturbed by an angle $\beta$.
Net restoring pressure
$\Delta p=1.5 \rho g h+\rho g h=2.5 \rho g h$
This pressure will be equal at all sections of the liquid. Therefore, net restoring torque on the whole liquid.
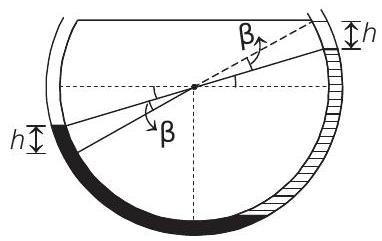
$$ \begin{aligned} \tau & =-(\Delta p)(A)(R) \\ \text { or } \tau & =-2.5 \rho g h A R \\ & =-2.5 \rho g A R[R \sin (\theta+\beta)-R \sin \theta] \\ & =-2.5 \rho g A R^{2}[\sin \theta \cos \beta+\sin \beta \cos \theta-\sin \theta] \end{aligned} $$
Assuming $\cos \beta \approx 1$ and $\sin \beta \approx \beta$ (as $\beta$ is small)
$$ \begin{aligned} & \therefore \quad \tau=-\left(2.5 \rho A g R^{2} \cos \theta\right) \beta \\ & \text { or } \quad I \alpha=-\left(2.5 \rho A g R^{2} \cos \theta\right) \beta \end{aligned} $$
Here, $\quad I=\left(m _1+m _2\right) R^{2}$
$$ =\frac{\pi R}{2} \cdot A \rho+\frac{\pi R}{2} \cdot A(1.5 \rho) R^{2} $$
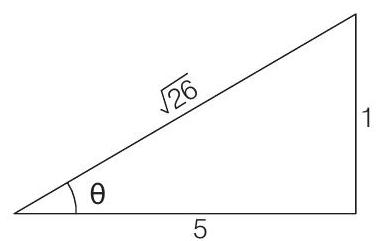
$$ \begin{aligned} & =\left(1.25 \pi R^{3} \rho\right) A \\ \text { and } \quad \cos \theta & =\frac{5}{\sqrt{26}}=0.98 \end{aligned} $$
Substituting in Eq. (i), we have $\alpha=-\frac{(6.11) \beta}{R}$
As angular acceleration is proportional to $-\beta$, motion is simple harmonic in nature.
$$ T=2 \pi \sqrt{\left|\frac{\beta}{\alpha}\right|}=2 \pi \sqrt{\frac{R}{6.11}} $$






