SATHEE: Simple Harmonic Motion 3 Question 13

Simple Harmonic Motion 3 Question 13

13. An ideal gas is enclosed in a vertical cylindrical container and supports a freely moving piston of mass $M$ . The piston and the cylinder have equal cross-sectional area $A$ . Atmospheric pressure is $p_{0}$ and when the piston is in equilibrium, the volume of the gas is $V_{0}$ . The piston is now displaced slightly from its equilibrium position. Assuming that the system is completely isolated from its surroundings, show that the piston executes simple harmonic motion and find the frequency of oscillation.

(1981, 6M)

Show Answer

Answer:

Correct Answer: 13. $\frac{1}{2 π} \sqrt{\frac{Y (p_{0} A^{2} + M g A)}{V_{0} M}}$

Solution:

In equilibrium pressure inside the cylinder $=$ pressure just outside it

$p = p_{0} + \frac{M g}{A}$

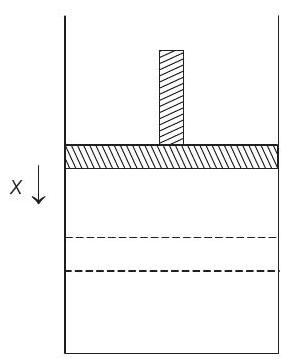
When piston is displaced slightly by an amount $x$ , change in volume,

$d V = - A x$

Since, the cylinder is isolated from the surroundings, process is adiabatic in nature. In adiabatic process,

$\frac{d p}{d V} = - \lor \frac{p}{V}$

or increase in pressure inside the cylinder,

$d p = - \frac{(⋁ p)}{V} (d V) = γ \frac{p_{0} + \frac{M g}{A}}{V_{0}} (A x)$

This increase in pressure when multiplied with area of cross-section $A$ will give a net upward force (or the restoring force). Hence,

or $a = \frac{F}{M} = - γ \frac{p_{0} A^{2} + M g A}{V_{0} M} x$

$\begin{aligned} F & = - (d p) A = - γ \frac{p_{0} A^{2} + M g A}{V_{0}} x \\ a & = \frac{F}{M} = - γ \frac{p_{0} A^{2} + M g A}{V_{0} M} x \end{aligned}$

Since, $a \propto - x$ , motion of the piston is simple harmonic in nature. Frequency of this oscillation is given by

$f = \frac{1}{2 π} \sqrt{| \frac{a}{x} |} = \frac{1}{2 π} \sqrt{\frac{Y (p_{0} A^{2} + M g A)}{V_{0} M}}$

Simple Harmonic Motion 3 Question 13

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Simple Harmonic Motion 3 Question 13

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu