SATHEE: Rotation 5 Question 19

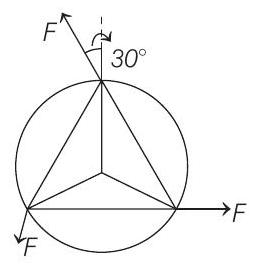
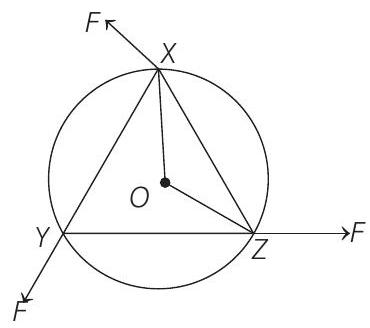
Rotation 5 Question 19

31. A uniform circular disc of mass $1.5 k g$ and radius $0.5 m$ is initially at rest on a horizontal frictionless surface. Three forces of equal magnitude $F = 0.5 N$ are applied simultaneously along the three sides of an equilateral triangle

$X Y Z$ with its vertices on the perimeter of the disc (see figure). One second after applying the forces, the angular speed of the disc in ${rad s}^{- 1}$ is (2012)

Fill in the Blanks

Show Answer

Answer:

Correct Answer: 31. (2)

Solution:

Angular impulse $=$ change in angular momentum

$\begin{aligned} ∴ \int τ d t = I ω \\ \Rightarrow ω = \frac{\int τ d t}{I} = \frac{\int_{0}^{t} 3 F \sin 30^{\circ} R d t}{I} \end{aligned}$

Substituting the values, we have

$ω = \frac{3 (0.5) (0.5) (0.5) (1)}{\frac{1.5 (0.5)^{2}}{2}} = 2 r a d / s$

Play Store

App Store

Ask SATHEE

Welcome to SATHEE !
Select from 'Menu' to explore our services, or ask SATHEE to get started. Let's embark on this journey of growth together! 🌐📚🚀🎓

I'm relatively new and can sometimes make mistakes.
If you notice any error, such as an incorrect solution, please use the thumbs down icon to aid my learning.
To begin your journey now, click on "I understand".

Rotation 5 Question 19

31. A uniform circular disc of mass 1.5kg and radius 0.5m is initially at rest on a horizontal frictionless surface. Three forces of equal magnitude F=0.5N are applied simultaneously along the three sides of an equilateral triangle

Fill in the Blanks

Answer:

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu

31. A uniform circular disc of mass $1.5 k g$ and radius $0.5 m$ is initially at rest on a horizontal frictionless surface. Three forces of equal magnitude $F = 0.5 N$ are applied simultaneously along the three sides of an equilateral triangle