Rotation 5 Question 12
22. A rigid uniform bar $A B$ of length $L$ is slipping from its vertical position on a frictionless floor (as shown in the figure). At some instant of time, the angle made by the bar with the vertical is $\theta$. Which of the following statements about its motion is/are correct?
(2017 Adv.)
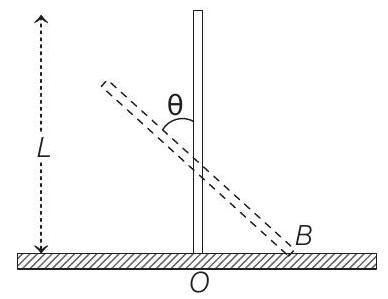
(a) Instantaneous torque about the point in contact with the floor is proportional to $\sin \theta$
(b) The trajectory of the point $A$ is parabola
(c) The mid-point of the bar will fall vertically downward
(d) When the bar makes an angle $\theta$ with the vertical, the displacement of its mid-point from the initial position is proportional to $(1-\cos \theta)$
Matching Type Questions
Show Answer
Answer:
Correct Answer: 22. (a,c,d)
Solution:
- When the bar makes an angle $\theta$, the height of its COM (mid-point) is $\frac{L}{2} \cos \theta$.
$\therefore \quad$ Displacement $=L-\frac{L}{2} \cos \theta=\frac{L}{2}(1-\cos \theta)$
Since, force on COM is only along the vertical direction, hence COM is falling vertically downward. Instantaneous torque about point of contact is
or
$$ \tau=m g \times \frac{L}{2} \sin \theta $$
$\tau \propto \sin \theta$
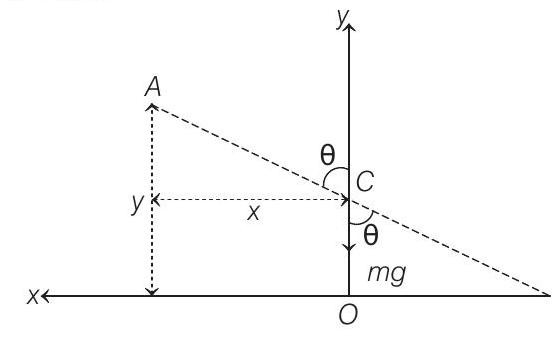
Now,
$$ \begin{aligned} x & =\frac{L}{2} \sin \theta \\ y & =L \cos \theta \\ \frac{x^{2}}{(L / 2)^{2}}+\frac{y^{2}}{L^{2}} & =1 \end{aligned} $$
Path of $A$ is an ellipse.






