Rotation 3 Question 16
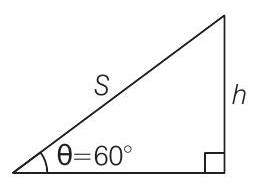
22. A ring and a disc are initially at rest, side by side, at the top of an inclined plane which makes an angle $60^{\circ}$ with the horizontal. They start to roll without slipping at the same instant of time along the shortest path. If the time difference between their reaching the ground is $(2-\sqrt{3}) / \sqrt{10} s$, then the height of the top of the inclined plane, in metres, is (Take, $g=10 ms^{-2}$ ) (2018 Main)
Fill in the Blanks
Show Answer
Answer:
Correct Answer: 22. (0.75)
Solution:
$$ \begin{array}{rlr} a & =\frac{g \sin \theta}{1+\frac{I}{M R^{2}}} & \\ a _{\text {ring }} & =\frac{g \sin \theta}{2} & \left(I=M R^{2}\right) \\ a _{\text {disc }} & =\frac{2 g \sin \theta}{3} & I=\frac{M R^{2}}{2} \end{array} $$
$$ \begin{aligned} s & =\frac{h}{\sin \theta}=\frac{1}{2} a t^{2} \\ & =\frac{1}{2} \frac{g \sin \theta}{2} t _1^{2} \\ \Rightarrow \quad t _1 & =\sqrt{\frac{4 h}{g \sin ^{2} \theta}}=\sqrt{\frac{16 h}{3 g}} \\ s & =\frac{h}{\sin \theta}=\frac{1}{2} a t^{2}=\frac{1}{2} \frac{2 g \sin \theta}{3} t _2^{2} \\ \Rightarrow \quad t _2 & =\sqrt{\frac{3 h}{g \sin ^{2} \theta}}=\sqrt{\frac{4 h}{g}} \\ t _2-t _1 & =\sqrt{\frac{16 h}{3 g}-\sqrt{\frac{4 h}{g}}=\frac{2-\sqrt{3}}{\sqrt{10}}} \\ \sqrt{h} \frac{4}{\sqrt{3}}-2 & =2-\sqrt{3} \end{aligned} $$
$$ \begin{aligned} \text { or } & \frac{3 f}{m} & =\omega^{2} A \\ \therefore & f & =\frac{M \omega^{2} A}{3} \\ \therefore & \tau _{\max }=f R & =\frac{M \omega^{2} A R}{3} \end{aligned} $$






