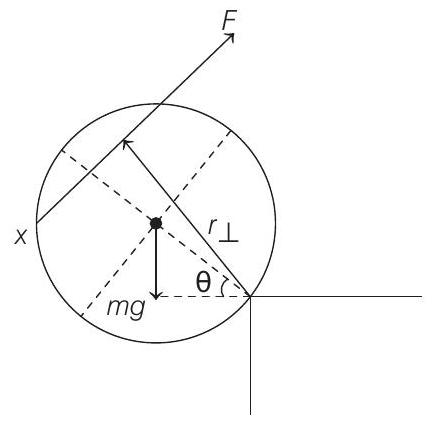
Rotation 3 Question 11
17. A wheel of radius
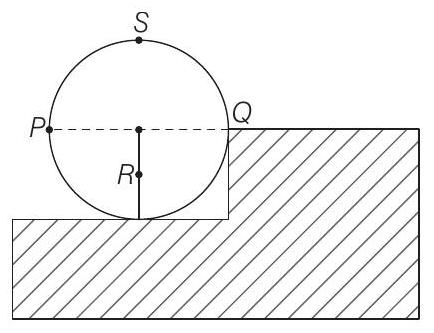axis normal to the plane of the paper passing through the point
(a) If the force is applied normal to the circumference at point
(b) If the force is applied tangentially at point
(c) If the force is applied at point
(d) If the force is applied normal to the circumference at point
Show Answer
Answer:
Correct Answer: 17. (a, c)
Solution:
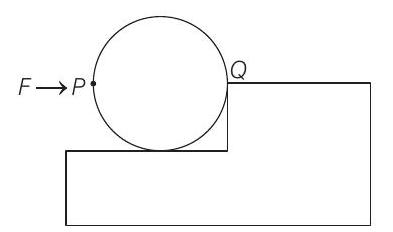
(a) If force is applied normal to surface at
(b) Wheel can climb.
(c)
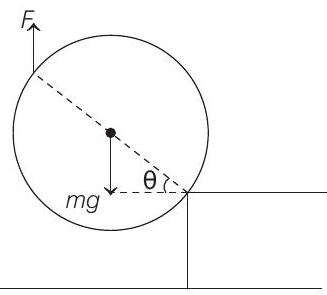
Hence, as
(d)
