Properties of Matter 4 Question 3
5. On heating water, bubbles beings formed at the bottom of the vessel detach and rise. Take the bubbles to be spheres of radius $R$ and making a circular contact of radius $r$ with the bottom of the vessel. If $r«R$ and the surface tension of water is $T$, value of $r$ just before bubbles detach is (density of water is $\rho_w$ )
(2014 Main)
(a) $R^2 \sqrt{\frac{\rho_w g}{3 T}}$
(b) $R^2 \sqrt{\frac{\rho_w g}{6 T}}$
(c) $R^2 \sqrt{\frac{\rho_w g}{T}}$
(d) $R^2 \sqrt{\frac{3 \rho_w g}{T}}$
Show Answer
Answer:
Correct Answer: 5. (*)
Solution:
- The bubble will detach if,
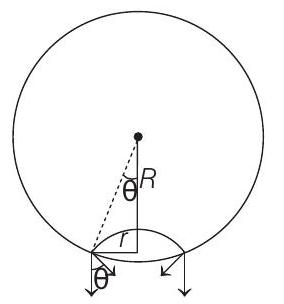
$\int \sin \theta T \times d l=T(2 \pi r) \sin \theta$
Buoyant force $\geq$ Surface tension force
$$ \begin{aligned} \frac{4}{3} \pi R^{3} \rho _w g & \geq \int T \times d l \sin \theta \\ \left(\rho _w\right)\left(\frac{4}{3} \pi R^{3}\right) g & \geq(T)(2 \pi r) \sin \theta \\ \sin \theta & =\frac{r}{R} \end{aligned} $$
Solving, $\quad r=\sqrt{\frac{2 \rho _w R^{4} g}{3 T}}=R^{2} \sqrt{\frac{2 \rho _w g}{3 T}}$
No option matches with the correct answer.






