Properties of Matter 4 Question 16
18. A soap bubble is being blown at the end of very narrow tube of radius
(2003, 4M)
Show Answer
Answer:
Correct Answer: 18.
Solution:
- Surface Tension force
Mass of the air per second entering the bubble
Momentum of air per second
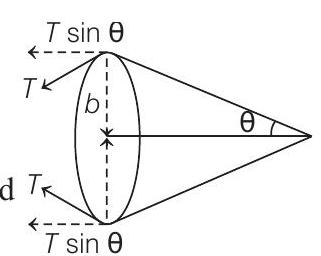
The bubble will separate from the tube when force due to moving air becomes equal to the surface tension force inside the bubble.
putting






