Properties of Matter 4 Question 13
15. Two soap bubbles $A$ and $B$ are kept in a closed chamber where the air is maintained at pressure $8 \mathrm{Nm}^{-2}$. The radii of bubbles $A$ and $B$ are $2 \mathrm{~cm}$, respectively. Surface tension of the soap-water used to make bubbles is $0.04 \mathrm{Nm}^{-1}$. Find the ratio $\frac{n_B}{n_A}$, where $n_A$ and $n_B$ are the number of moles of air in bubbles $A$ and $B$, respectively. [Neglect the effect of gravity]
(2009)
Show Answer
Answer:
Correct Answer: 15. 6
Solution:
- Although not given in the question, but we will have to assume that temperatures of $A$ and $B$ are same.
$$ \begin{aligned} \frac{n _B}{n _A} & =\frac{p _B V _B / R T}{p _A V _A / R T}=\frac{p _B V _B}{p _A V _A} \\ & =\frac{p+4 S / r _A \times 4 / 3 \pi\left(r _A\right)^{3}}{\left(p+4 S / r _B\right) \times 4 / 3 \pi\left(r _B\right)^{3}} \end{aligned} $$
$(S$ = surface tension $)$
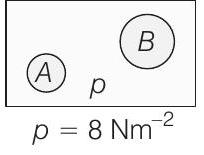
Substituting the values, we get
$$ \frac{n _B}{n _A}=6 $$
