Properties of Matter 3 Question 3
9. A uniform capillary tube of inner radius $r$ is dipped vertically into a beaker filled with water. The water rises to a height $h$ in the capillary tube above the water surface in the beaker. The surface tension of water is $\sigma$. The angle of contact between water and the wall of the capillary tube is $\theta$. Ignore the mass of water in the meniscus. Which of the following statements is (are) true?
(2018 Adv.)
(a) For a given material of the capillary tube, $h$ decreases with increase in $r$
(b) For a given material of the capillary tube, $h$ is independent of $\sigma$
(c) If this experiment is performed in a lift going up with a constant acceleration, then $h$ decreases
(d) $h$ is proportional to contact angle $\theta$
Passage Based Question
Passage 1
When liquid medicine of density $\rho$ is to be put in the eye, it is done with the help of a dropper. As the bulb on the top of the dropper is pressed, a drop forms at the opening of the dropper. We wish to estimate the size of the drop. We first assume that the drop formed at the opening is spherical because that requires a minimum increase in its surface energy. To determine the size, we calculate the net vertical force due to the surface tension $T$ when the radius of the drop is $R$. When this force becomes smaller than the weight of the drop, the drop gets detached from the dropper.
(2010)
Show Answer
Answer:
Correct Answer: 9. (c)
Solution:
- From conservation of energy
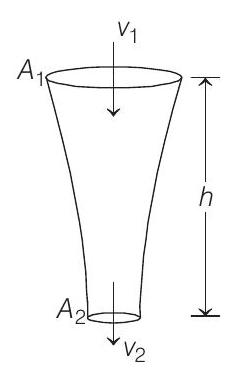
$$ v _2^{2}=v _1^{2}+2 g h $$
[can also be found by applying Bernoulli’s theorem] From continuity equation
$$ \begin{aligned} A _1 v _1 & =A _2 v _2 \\ v _2 & =\left(\frac{A _1}{A _2}\right) v _1 \end{aligned} $$
Substituting value of $v _2$ from Eq. (ii) in Eq. (i),
$$ \begin{array}{rlrl} & \frac{A _1^{2}}{A _2^{2}} \cdot v _1^{2} & =v _1^{2}+2 g h \text { or } A _2^{2}=\frac{A _1^{2} v _1^{2}}{v _1^{2}+2 g h} \\ \therefore \quad A _2 & =\frac{A _1 v _1}{\sqrt{v _1^{2}+2 g h}} \end{array} $$
Substituting the given values
$$ \begin{aligned} & A _2=\frac{\left(10^{-4}\right)(1.0)}{\sqrt{(1.0)^{2}+2(10)(0.15)}} \\ & A _2=5.0 \times 10^{-5} m^{2} \end{aligned} $$