Properties of Matter 2 Question 21
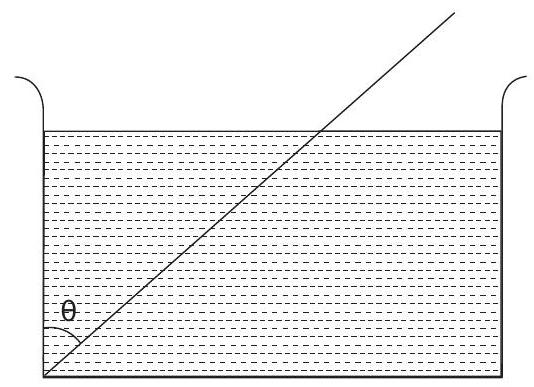
21. A wooden plank of length $1 m$ and uniform cross-section is hinged at one end to the bottom of a tank as shown in figure. The tank is filled with water upto a height $0.5 m$. The specific gravity of the plank is 0.5 . Find the angle $\theta$ that the plank makes with the vertical in the equilibrium position (exclude the case $\theta=0^{\circ}$ ).
$(1984,8 M)$
Show Answer
Answer:
Correct Answer: 21. $45^{\circ}$
Solution:
- Submerged length $=0.5 \sec \theta, F=$ Upthrust, $w=$ Weight
Three forces will act on the plank.
(a) Weight which will act at centre of plank.
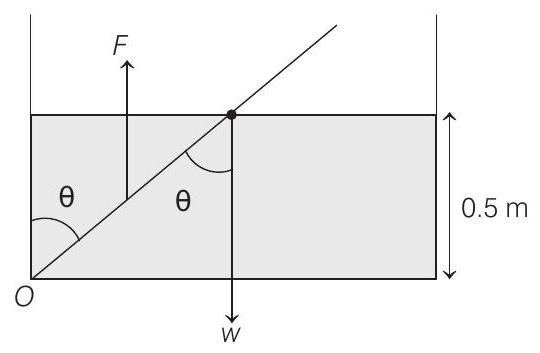
(b) Upthrust which will act at centre of submerged portion.
(c) Force from the hinge at $O$.
Taking moments of all three forces about point $O$.
Moment of hinge force will be zero.
$\therefore$ Moment of $w$ (clockwise)
$=$ Moment of $F$ (anti-clockwise)
$\therefore(A \lg \rho) \frac{l}{2} \sin \theta=A(0.5 \sec \theta)\left(\rho _w\right)(g)\left(\frac{0.5 \sec \theta}{2}\right) \sin \theta$
$\therefore \quad \cos ^{2} \theta=\frac{(0.5)^{2}(1)}{\left(l^{2}\right)(\rho)}$
$$ =\frac{(0.5)^{2}}{(0.5)}=\frac{1}{2} \quad(\text { as } l=1 m) $$
$\therefore \quad \cos \theta=\frac{1}{\sqrt{2}}$
or $ \theta=45^{\circ} $
