Properties of Matter 2 Question 20
20. A wooden stick of length $L$, radius $R$ and density $\rho$ has a small metal piece of mass $m$ (of negligible volume) attached to its one end. Find the minimum value for the mass $m$ (in terms of given parameters) that would make the stick float vertically in equilibrium in a liquid of density $\sigma(>\rho)$.
(1999, 10M)
Show Answer
Answer:
Correct Answer: 20. $\pi R^{2} L(\sqrt{\rho \sigma}-\rho)$
Solution:
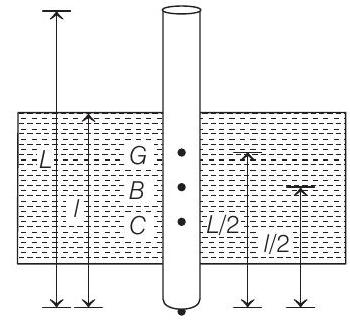
- Let $M=$ Mass of stick $=\pi R^{2} \rho L$
(i)
(ii)
(iii)
$l=$ Immersed length of the rod
$G=CM$ of $\operatorname{rod}$
$B=$ Centre of buoyant force $(F)$
$C=CM$ of $\operatorname{rod}+$ mass $(m)$
$Y _{CM}=$ Distance of $C$ from bottom of the rod
Mass $m$ should be attached to the lower end because otherwise $B$ will be below $G$ and $C$ will be above $G$ and the torque of the couple of two equal and opposite forces $F$ and $(M+m) g$ will be counter clockwise on displacing the rod leftwards. Therefore, the rod cannot be in rotational equilibrium. See the figure (iii).
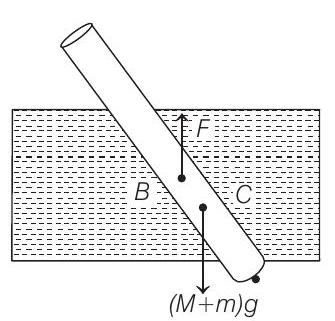
Now, refer figures (i) and (ii).
For vertical equilibrium $M g+m g=F$ (upthrust)
or $\left(\pi R^{2} L\right) \rho g+m g=\left(\pi R^{2} l\right) \sigma g$
$\therefore \quad l=\frac{\pi R^{2} L \rho+m}{\pi R^{2} \sigma}$
Position of CM ( of rod $+m$ ) from bottom
$$ Y _{CM}=\frac{M \cdot \frac{L}{2}}{M+m}=\frac{\left(\pi R^{2} L \rho\right) \frac{L}{2}}{\left(\pi R^{2} L \rho\right)+m} $$
Centre of buoyancy $(B)$ is at a height of $\frac{l}{2}$ from the bottom.
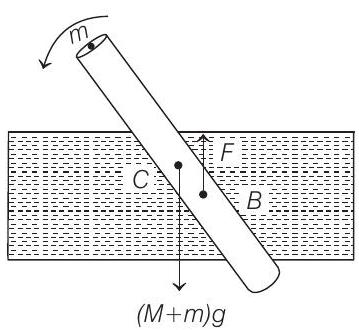
We can see from figure (ii) that for rotational equilibrium of the rod, $B$ should either lie above $C$ or at the same level of $B$.
Therefore, $\quad \frac{l}{2} \geq Y _{CM}$
$\begin{aligned} \text { or } & & \frac{\pi R^{2} L \rho+m}{2 \pi R^{2} \sigma} & \geq \frac{\left(\pi R^{2} L \rho\right) \frac{L}{2}}{\left(\pi R^{2} L \rho\right)+m} \\ \text { or } & & m+\pi R^{2} L \rho & \geq \pi R^{2} L \sqrt{\rho \sigma} \\ \text { or } & & m & \geq \pi R^{2} L(\sqrt{\rho \sigma}-\rho)\end{aligned}$
$\therefore$ Minimum value of $m$ is $\pi R^{2} L(\sqrt{\rho \sigma}-\rho)$.
