Optics 7 Question 42
43. A ray of light travelling in air is incident at grazing angle (Incident angle $=90^{\circ}$ ) on a long rectangular slab of a transparent medium of thickness $t=1.0 m$. The point of incidence is the origin $A(0,0)$. The medium has a variable index of refraction $n(y)$ given by
$$ n(y)=\left[k y^{3 / 2}+1\right]^{1 / 2} \text { where } k=1.0(m)^{-3 / 2} \text {. } $$
The refractive index of air is 1.0.
(1995, 10 M)
(a) Obtain a relation between the slope of the trajectory of the ray at a point $B(x, y)$ in the medium and the incident angle at that point.
(b) Obtain an equation for the trajectory $y(x)$ of the ray in the medium.
(c) Determine the coordinates $\left(x _1, y _1\right)$ of the point $P$, where the ray intersects the upper surface of the slab-air boundary.
(d) Indicate the path of the ray subsequently.
Show Answer
Answer:
Correct Answer: 43. (a) Slope $=\cot i$
(b) $4 y^{1 / 4}=x$
(c) $(4 m, 1 m)$
(d) the ray will emerge grazingly
Solution:
- (a) Refractive index is a function of $y$. It varies along $Y$-axis i.e. the boundary separating two media is parallel to $X$-axis or normal at any point will be parallel to $Y$-axis.
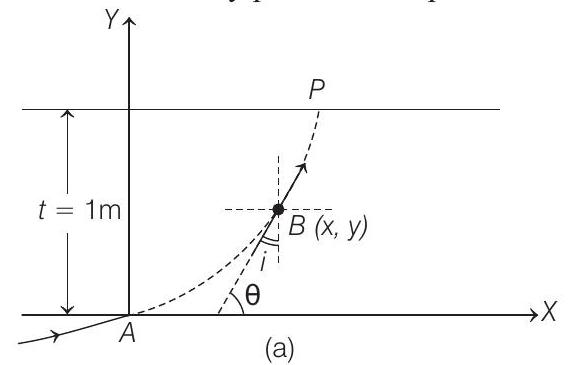
Secondly, refractive index increases as $y$ is increased. Therefore, ray of light is travelling from rarer to denser medium i.e. it will bend towards the normal and shape of its trajectory will be as shown below.
(b)
Now, refer to figure (a)
Let $i$ be the angle of incidence at any point $B$ on its path
$$ \theta=90^{\circ}-i \text { or } \tan \theta=\tan \left(90^{\circ}-i\right)=\cot i $$
or slope $=\cot i$
(b) but $\tan \theta=\frac{d y}{d x} \Rightarrow \therefore \quad \frac{d y}{d x}=\cot i$
Applying Snell’s law at $A$ and $B$
$n _A \sin i _A=n _B \sin i _B \Rightarrow n _A=1$ because $y=0$
$\sin i _A=1$ because $i _A=90^{\circ}$
(Grazing incidence)
$$ n _B=\sqrt{k y^{3 / 2}+1}=\sqrt{y^{3 / 2}+1} $$
because $k=1.0(m)^{-3 / 2}$
$\therefore \quad(1)(1)=\sqrt{\left(y^{3 / 2}+1\right)} \sin i \Rightarrow \sin i=\frac{1}{\sqrt{y^{3 / 2}+1}}$
$\therefore \quad \cot i=\sqrt{y^{3 / 2}}$ or $y^{3 / 4}$
Equating Eqs. (i) and (ii), we get
$$ \begin{array}{r} \frac{d y}{d x}=y^{3 / 4} \text { or } y^{-3 / 4} d y=d x \\ \text { or } \int _0^{y} y^{-3 / 4} d y=\int _0^{x} d x \quad \text { or } 4 y^{1 / 4}=x \end{array} $$
The required equation of trajectory is $4 y^{1 / 4}=x$.
(c) At point $P$, where the ray emerges from the slab
$$ \begin{array}{rlrl} & & y=1.0 m \\ \therefore & & x & =4.0 m \end{array} $$
Therefore, coordinates of point $P$ are
$$ P=(4.0 m, 1.0 m) $$
(d) As $n _A \sin i _A=n _P \sin i _p$ and as $n _A=n _P=1$
Therefore, $i _P=i _A=90^{\circ}$ i.e. the ray will emerge parallel to the boundary at $P$ i.e. at grazing emergence.






