Optics 7 Question 41
42. A thin equiconvex lens of glass of refractive index $\mu=3 / 2$ and of focal length $0.3 m$ in air is sealed into an opening at one end of a tank filled with water $\mu=4 / 3$. On the opposite side of the lens, a mirror is placed inside the tank on the tank wall perpendicular to the lens axis, as shown in figure. The separation between the lens and the mirror is $0.8 m$. A small object is placed outside the tank in front of lens. Find the position (relative to the lens) of the image of the object formed by the system
(1997C, 5M)
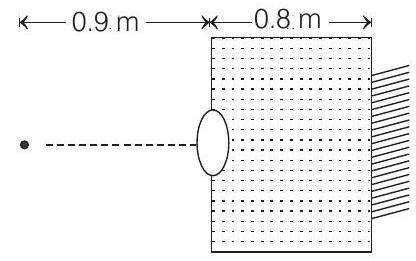
Show Answer
Answer:
Correct Answer: 42. $0.9 m$ from the lens (rightwards) or $0.1 m$ behind the mirror
Solution:
- From lens maker’s formula,
$$ \frac{1}{f}=(\mu-1) \frac{1}{R _1}-\frac{1}{R _2} $$
we have $\quad \frac{1}{0.3}=\frac{3}{2}-1 \quad \frac{1}{R}-\frac{1}{-R}$
$$ \text { (Here, } R _1=R \text { and } R _2=-R \text { ) } $$
$$ R=0.3 $$
Now applying $\frac{\mu _2}{v}-\frac{\mu _1}{u}=\frac{\mu _2-\mu _1}{R}$ at air glass surface, we get
$$ \frac{3 / 2}{v _1}-\frac{1}{-(0.9)}=\frac{3 / 2-1}{0.3} $$
$$ \therefore \quad v _1=2.7 m $$
i.e. first image $I _1$ will be formed at $2.7 m$ from the lens. This will act as the virtual object for glass water surface. Therefore, applying $\frac{\mu _2}{v}-\frac{\mu _1}{u}=\frac{\mu _2-\mu _1}{R}$ at glass water surface, we have
$$ \begin{array}{rlrl} & \frac{4 / 3}{v _2}-\frac{3 / 2}{2.7} & =\frac{4 / 3-3 / 2}{-0.3} \\ \therefore \quad v _2 & =1.2 m \end{array} $$
i.e. second image $I _2$ is formed at $1.2 m$ from the lens or $0.4 m$ from the plane mirror. This will act as a virtual object for mirror. Therefore, third real image $I _3$ will be formed at a distance of $0.4 m$ in front of the mirror after reflection from it. Now this image will work as a real object for water-glass interface. Hence, applying
$$ \begin{aligned} \frac{\mu _2}{v}-\frac{\mu _1}{u} & =\frac{\mu _2-\mu _1}{R} \\ \text { we get } \frac{3 / 2}{v _4}-\frac{4 / 3}{-(0.8-0.4)} & =\frac{3 / 2-4 / 3}{0.3} \\ \therefore \quad v _4 & =-0.54 m \end{aligned} $$
i.e. fourth image is formed to the right of the lens at a distance of $0.54 m$ from it. Now finally applying the same formula for glass-air surface,
$$ \begin{array}{rlrl} \therefore \quad & \frac{1}{v _5}-\frac{3 / 2}{-0.54} & =\frac{1-3 / 2}{-0.3} \\ v _5 & =-0.9 m \end{array} $$
i.e. position of final image is $0.9 m$ relative to the lens (rightwards) or the image is formed $0.1 m$ behind the mirror.






