Optics 6 Question 32
34. Two coherent monochromatic point sources
(2017 Adv.)
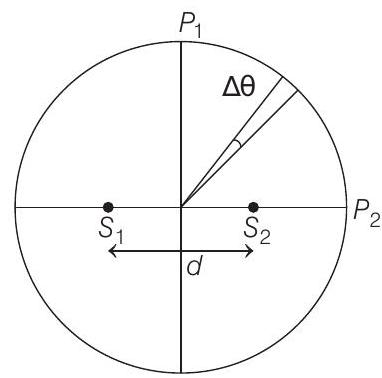
(a) The angular separation between two consecutive bright spots decreases as we move from
(b) A dark spot will be formed at the point
(c) The total number of fringes produced between
(d) At
Show Answer
Solution:
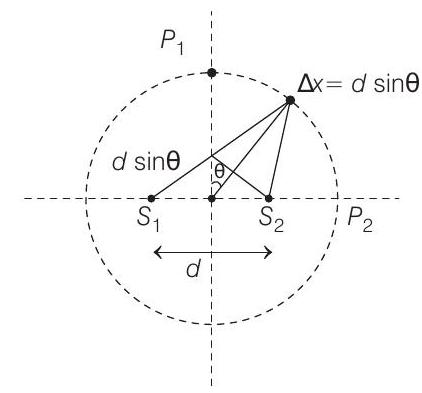
at
Number of maximas will be
Hence, bright fringe will be formed.
At
For (a) option
As we move from






