Optics 6 Question 1
1. A system of three polarisers $P _1, P _2, P _3$ is set up such that the pass axis of $P _3$ is crossed with respect to that of $P _1$. The pass axis of $P _2$ is inclined at $60^{\circ}$ to the pass axis of $P _3$. When a beam of unpolarised light of intensity $I _0$ is incident on $P _1$, the intensity of light transmitted by the three polarisers is $I$. The ratio $\left(I _0 / I\right)$ equals (nearly)
(2019 Main, 12 April II)
(a) 5.33
(b) 16.00
(c) 10.67
(d) 1.80
Show Answer
Answer:
Correct Answer: 1. (c)
Solution:
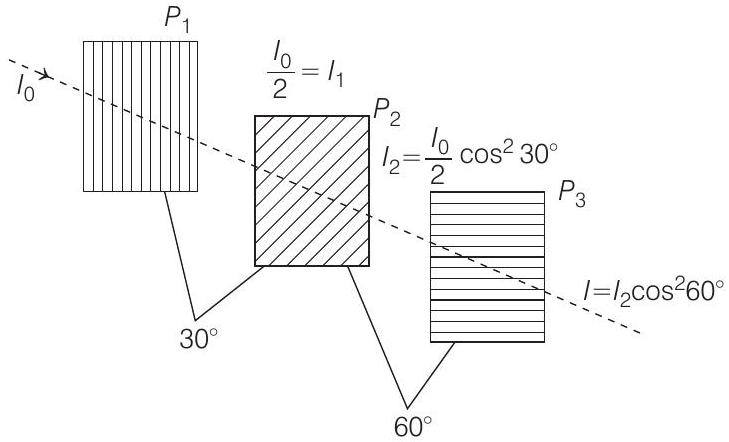
When unpolarised light pass through polaroid $P _1$, intensity obtained is
$ I _1=\frac{I _0}{2} $
where, $I _0=$ intensity of incident light.
Now, this transmitted light is polarised and it pass through polariser $P _2$. So, intensity $I _2$ transmitted is obtained by Malus law.
$ \Rightarrow \quad I _2=I _1 \cos ^{2} \theta $
As angle of pass axis of $P _1$ and $P _3$ is $90^{\circ}$ and angle of pass axis of $P _2$ and $P _3$ is $60^{\circ}$, so angle between pass axis of $P _1$ and $P _2$ is $\left(90^{\circ}-60^{\circ}\right)=30^{\circ}$. So,
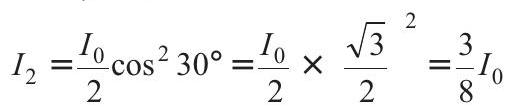
When this light pass through third polariser $P _3$, intensity $I$ transmitted is again obtained by Malus law.
So, $I=I _2 \cos ^{2} 60^{\circ}=\frac{3}{8} I _0 \quad \cos ^{2} 60^{\circ}$
$ =\frac{3}{8} I _0 \times \frac{1}{2}^{2}=\frac{3}{32} I _0 $
So, ratio $\frac{I _0}{I}=\frac{32}{3}=10.67$
