Optics 3 Question 40
40. The radius of curvature of the convex face of a planoconvex lens is $12 cm$ and its $\mu=1.5$.
(1979)
(a) Find the focal length of the lens. The plane face of the lens is now silvered.
(b) At what distance from the lens will parallel rays incident on the convex surface converge?
(c) Sketch the ray diagram to locate the image, when a point object is placed on the axis $20 cm$ from the lens.
(d) Calculate the image distance when the object is placed as in (c)
Show Answer
Answer:
Correct Answer: 40. (a) + 24 cm (b) at 12 cm (d) v = - 30 cm
Solution:
- (a) $\frac{1}{f}=(\mu-1) \frac{1}{R _1}-\frac{1}{R _2}=(1.5-1) \frac{1}{12}-\frac{1}{\infty}=\frac{1}{24}$
$\therefore f=+24 cm$
(b) The system will behave like a mirror of power given by
$$ \begin{aligned} P = 2 P_L + P_M \\ \therefore \quad-\frac{1}{F(m)} & =2 \Big[\frac{1}{0.24}\Big]+0 \\ \therefore \quad F & =-0.12 m=-12 cm \end{aligned} $$
Hence, the system will behave like a concave mirror of focal length $12 cm$. Therefore parallel rays will converge at a distance of $12 cm$ (to the left) of the system.
(c)
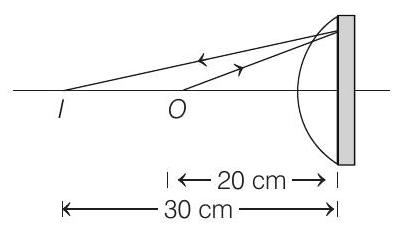
(d) Using mirror formula
$$ \frac{1}{v}-\frac{1}{20}=\frac{-1}{12} $$
Solving, we get $v=-30 cm$.
Therefore the image will be formed at a distance of $30 cm$ to the left of system.






