Optics 3 Question 26
26. A plano-convex lens is made of material of refractive index $n$. When a small object is placed $30 cm$ away in front of the curved surface of the lens, an image of double the size of the object is produced. Due to reflection from the convex surface of the lens, another faint image is observed at a distance of 10 $cm$ away from the lens. Which of the following statement(s) is (are) true?
(2016 Adv.)
(a) The refractive index of the lens is 2.5
(b) The radius of curvature of the convex surface is $45 cm$
(c) The faint image is erect and real
(d) The focal length of the lens is $20 cm$
Show Answer
Answer:
Correct Answer: 26. (a, d)
Solution:
- Case 1
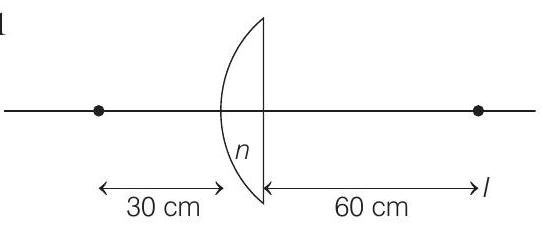
Using lens formula,
$$ \begin{aligned} \Rightarrow \quad \frac{1}{60}+\frac{1}{30} & =\frac{1}{f _1} \Rightarrow \frac{1}{f _1}=\frac{1}{60}+\frac{2}{60} \\ f _1 & =20 cm \end{aligned} $$
Further, $\frac{1}{f _1}=(n-1) \frac{1}{R}-\frac{1}{\infty} \Rightarrow f _1=\frac{R}{n-1}=+20 cm$
Case 2
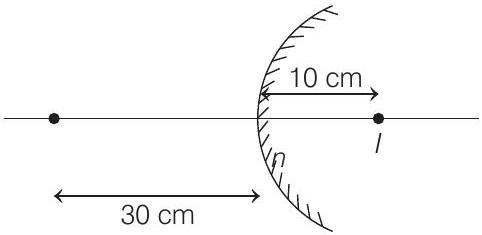
Using mirror formula
$$ \begin{gathered} \frac{1}{10}-\frac{1}{30}=\frac{1}{f _2} \\ \frac{3}{30}-\frac{1}{30}=\frac{1}{f _2}=\frac{2}{30} \\ f _2=15=\frac{R}{2} \Rightarrow R=30 \\ R=30 cm \\ \frac{R}{n-1}+20 cm=\frac{30}{n-1} \\ \Rightarrow \quad=2 n-2=3 \Rightarrow f _1=+20 cm \end{gathered} $$
Refractive index of lens is 2.5 .
Radius of curvature of convex surface is $30 cm$.
Faint image is erect and virtual focal length of lens is $20 cm$.
