Optics 3 Question 21
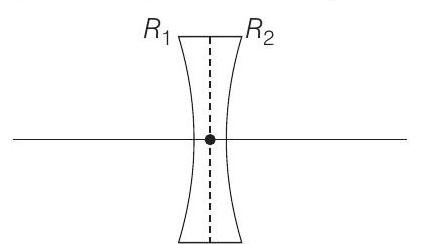
21. A concave lens of glass, refractive index 1.5 has both surfaces of same radius of curvature $R$. On immersion in a medium of refractive index 1.75 , it will behave as a
$(1999,2 M)$
(a) convergent lens of focal length $3.5 R$
(b) convergent lens of focal length $3.0 R$
(c) divergent lens of focal length $3.5 R$
(d) divergent lens of focal length $3.0 R$
Show Answer
Answer:
Correct Answer: 21. (a)
Solution:
- $R _1=-R, R _2=+R, \mu _g=1.5$ and $\mu _m=1.75$
$$ \therefore \quad \frac{1}{f}=\Big(\frac{\mu _g}{\mu _m}-1\Big) \quad \Big(\frac{1}{R _1}-\frac{1}{R _2}\Big) $$
Substituting the values, we have
$$ \begin{array}{rlrl} & & \frac{1}{f} & =\Big(\frac{1.5}{1.75}-1\Big) \quad \Big(\frac{1}{-R}-\frac{1}{R}\Big)=\frac{1}{3.5 R} \\ \therefore & f & =+3.5 R \end{array} $$
Therefore, in the medium it will behave like a convergent lens of focal length 3.5R. It can be understood as, $\mu _m>\mu _g$, the lens will change its behaviour.






