Optics 2 Question 30
29. A parallel beam of light travelling in water (refractive index $=4 / 3$ ) is refracted by a spherical air bubble of radius $2 mm$ situated in water. Assuming the light rays to be paraxial.
$(1988,6 M)$
(a) Find the position of the image due to refraction at the first surface and the position of the final image.
(b) Draw a ray diagram showing the positions of both the images.
Show Answer
Answer:
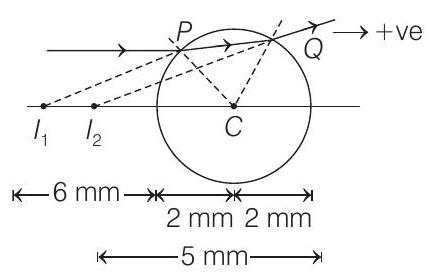
Correct Answer: 29. (a) $-6 mm,-5 mm$
Solution:
- (a)
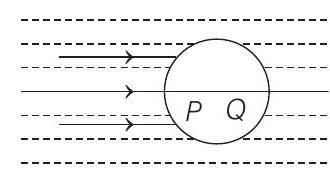
Applying $\frac{\mu _2}{v}-\frac{\mu _1}{u}=\frac{\mu _2-\mu _1}{R}$, one by one on two spherical surfaces.
First on left surface
$$ \begin{aligned} \frac{1}{v _1}-\frac{4 / 3}{\infty} & =\frac{1-4 / 3}{+2} \\ \frac{1}{v _1} & =-\frac{1}{6} \\ v _1 & =-6 mm \end{aligned} $$
i.e. first image will be formed at $6 mm$ towards left of $P$
Second on right surface Now, distance of first image $I _1$ from $Q$ will be $10 mm$ (towards left).
$$ \begin{aligned} \frac{4 / 3}{v _2}-\frac{1}{-10} & =\frac{4 / 3-1}{-2} \\ \frac{4}{3 v _2} & =-\frac{1}{6}-\frac{1}{10}=-\frac{4}{15} \\ v _2 & =-5 mm \end{aligned} $$
or
(b) The ray diagram is shown in figure.
NOTE
- At $P$ and $Q$ both normal will pass through $C$.
- At $P$ ray of light is travelling from a denser medium (water) to rarer medium (air) therefore, ray of light will bend away from the normal and on extending meet at $l _1$. Similarly at $Q$, ray of light bends towards the normal.
- Both the images $I _1$ and $I _2$ are virtual.






