Optics 2 Question 27
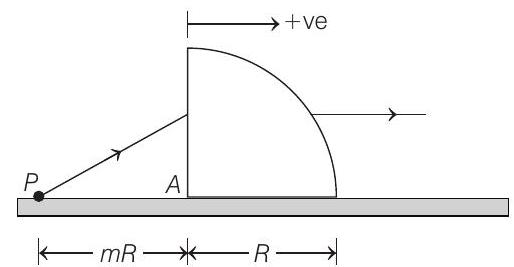
26. A quarter cylinder of radius $R$ and refractive index 1.5 is placed on a table. A point object $P$ is kept at a distance of $m R$ from it. Find the value of $m$ for which a ray from $P$ will emerge parallel to the table as shown in figure. $\quad(1999,5 M)$
Show Answer
Answer:
Correct Answer: 26. $\frac{4}{3}$
Solution:
- Applying $\frac{\mu _2}{v}-\frac{\mu _1}{u}=\frac{\mu _2-\mu _1}{R}$
First on plane surface
$$ \begin{aligned} \frac{1.5}{A I _1}-\frac{1}{-m R} & =\frac{1.5-1}{\infty}=0 \\ A I _1 & =-(1.5 mR) \end{aligned} $$
$(R=\infty)$
$\therefore \quad A I _1=-(1.5 mR)$
Then, on curved surface
$$ \frac{1}{\infty}-\frac{1.5}{-(1.5 m R+R)}=\frac{1-1.5}{-R} $$
$[v=\infty$, because final image is at infinity]
$\Rightarrow \quad \frac{1.5}{(1.5 m+1) R}=\frac{0.5}{R}$
$\Rightarrow \quad 3=1.5 m+1$
$\Rightarrow \quad \frac{3}{2} m=2$
or $\quad m=\frac{4}{3}$






