Optics 2 Question 23
23. For two structures namely $S _1$ with $n _1=\frac{\sqrt{45}}{4}$ and $n _2=\frac{3}{2}$, and $S _2$ with $n _1=\frac{8}{5}$ and $n _2=\frac{7}{5}$ and taking the refractive index of water to be $\frac{4}{3}$ and that to air to be 1 , the correct options is/are
(2015 Adv.)
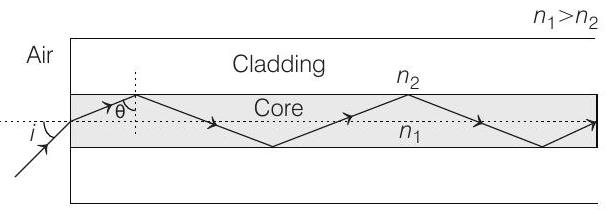
(a) $N A$ of $S _1$ immersed in water is the same as that of $S _2$ immersed in a liquid of refractive index $\frac{16}{3 \sqrt{15}}$
(b) $N A$ of $S _1$ immersed in liquid of refractive index $\frac{6}{\sqrt{15}}$ is the same as that of $S _2$ immersed in water
(c) NA of $S _1$ placed in air is the same as that $S _2$ immersed in liquid of refractive index $\frac{4}{\sqrt{15}}$
(d) $N A$ of $S _1$ placed in air is the same as that of $S _2$ placed in water
Show Answer
Answer:
Correct Answer: 23. $(a, c)$
Solution:
- $\frac{4}{3} \sin i=\frac{\sqrt{45}}{4} \sin \left(90-\theta _c\right)=\frac{\sqrt{45}}{4} \cos \theta _c$
$$ \sin \theta _c=\frac{n _2}{n _1} $$
$\therefore \quad \cos \theta _c=\sqrt{1-{\frac{n _2}{n _1}}^{2}}$
$\Rightarrow \quad \frac{4}{3} \sin i=\frac{\sqrt{45}}{4} \frac{3}{\sqrt{45}}$
$$ \sin i=\frac{9}{16} $$
In second case,
$$ \begin{array}{r} \sin \theta _c=\frac{n _2}{n _1}=\frac{7}{8} \Rightarrow \cos \theta _c=\frac{\sqrt{15}}{8} \\ \frac{16}{3 \sqrt{15}} \sin i=\frac{8}{5} \sin \left(90-\theta _c\right) \end{array} $$
Simplifying we get,
$$ \sin i=\frac{9}{16} $$
Same approach can be adopted for other options. Correct answers are (a) and (c).






