Optics 2 Question 12
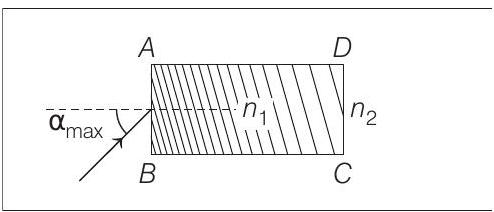
12. A rectangular glass slab $A B C D$ of refractive index $n _1$ is immersed in water of refractive index $n _2\left(n _1>n _2\right)$. A ray of light is incident at the surface $A B$ of the slab as shown. The maximum value of the angle of incidence $\alpha _{\max }$, such that the ray comes out only from the other surface $C D$, is given by
$(2000,2 M)$
(a) $\sin ^{-1} \Big[\frac{n _1}{n _2} \cos \Big(\sin ^{-1} \frac{n _2}{n _1}\Big)\Big]$
(b) $\sin ^{-1} \Big[n _1 \cos \Big(\sin ^{-1} \frac{1}{n _2}\Big)\Big]$
(c) $\sin ^{-1} \Big[\frac{n _1}{n _2}\Big]$
(d) $\sin ^{-1} \Big[\frac{n _2}{n _1}\Big]$
Show Answer
Answer:
Correct Answer: 12. (a)
Solution:
- Rays come out only from $C D$, means rays after refraction from $A B$ get total internally reflected at $A D$. From the figure
$$ \begin{gathered} r _1+r _2=90^{\circ} \\ r _1=90^{\circ}-r _2 \\ \quad\left(r _1\right) _{\max }=90^{\circ}-\left(r _2\right) _{\min } \text { and }\left(r _2\right) _{\min }=\theta _C \end{gathered} $$
(for total internal reflection at $A D$ )
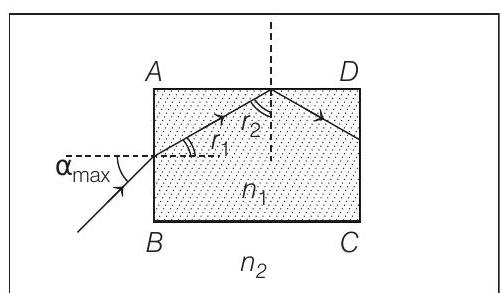
where,
$$ \sin \theta _C=\frac{n _2}{n _1} $$
$$ \begin{aligned} \text { or } & \theta _C & =\sin ^{-1} \frac{n _2}{n _1} \\ \therefore & \left(r _1\right) _{\max } & =90^{\circ}-\theta _C \end{aligned} $$
Now, applying Snell’s law at face $A B$
$$ \begin{aligned} \frac{n _1}{n _2} & =\frac{\sin \alpha _{\max }}{\sin \left(r _1\right) _{\max }} \\ & =\frac{\sin \alpha _{\max }}{\sin \left(90^{\circ}-\theta _C\right)} \end{aligned} $$
$$ \begin{aligned} & =\frac{\sin \alpha _{\max }}{\cos \theta _C} \\ \text { or } \quad \sin \alpha _{\max } & =\frac{n _1}{n _2} \cos \theta _C \\ \therefore \quad \alpha _{\max } & =\sin ^{-1} \Big[\frac{n _1}{n _2} \cos \theta _C \Big] \\ & =\sin ^{-1} \Big[\frac{n _1}{n _2} \cos \Big(\sin ^{-1} \frac{n _2}{n _1}\Big)\Big] \end{aligned} $$
