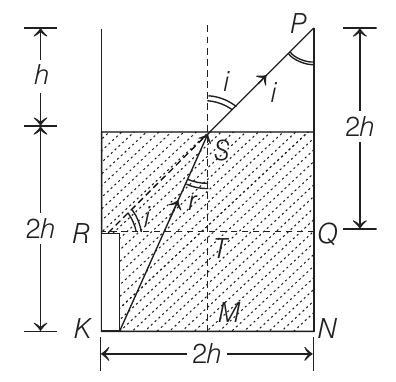
Optics 2 Question 10
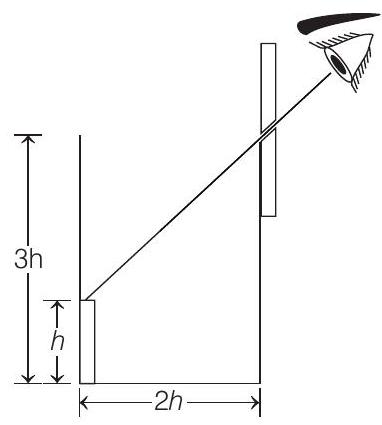
10. An observer can see through a pin-hole the top end of a thin rod of height
(2002, 2M)
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 10. (b)
Solution: