Optics 2 Question 1
1. A transparent cube of side $d$, made of a material of refractive index $\mu _2$, is immersed in a liquid of refractive index $\mu _1\left(\mu _1<\mu _2\right)$. A ray is incident on the face $A B$ at an angle $\theta$ (shown in the figure). Total internal reflection takes place at point $E$ on the face $B C$. Then, $\theta$ must satisfy
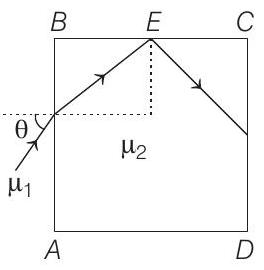
(2019 Main, 12 April II)
(a) $\theta<\sin ^{-1} \frac{\mu _1}{\mu _2}$
(b) $\theta>\sin ^{-1} \sqrt{\frac{\mu _2^{2}}{\mu _1^{2}}-1}$
(c) $\theta<\sin ^{-1} \sqrt{\frac{\mu _2^{2}}{\mu _1^{2}}-1}$
(d) $\theta>\sin ^{-1} \frac{\mu _1}{\mu _2}$
Show Answer
Answer:
Correct Answer: 1. (c)
Solution:
- Key Idea
The critical angle is defined as the angle of incidence that provides an angle of refraction of $90^{\circ}$.
$$ \text { So, } \quad \theta _c=\sin ^{-1} \frac{\mu _2}{\mu _1} $$
For total internal reflection, angle of incidence $(i)$ at medium interface must be greater than critical angle $(C)$.
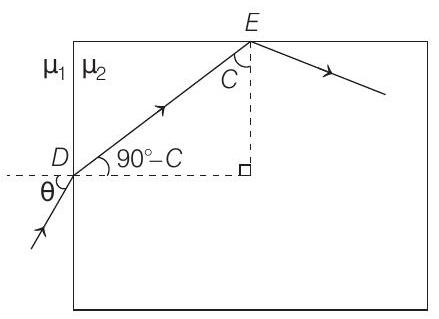
where,
$$ \sin C=\frac{\mu _1}{\mu _2} \cdots(i) $$
Now, in given arrangement,
at point $D$,
$$ \begin{gathered} \frac{\sin i}{\sin r}=\frac{\mu _2}{\mu _1} \quad \text { (Snell’s law) } \\ \Rightarrow \quad \frac{\sin \theta}{\sin \left(90^{\circ}-C\right)}=\frac{\mu _2}{\mu _1} \Rightarrow \frac{\sin \theta}{\cos C}=\frac{\mu _2}{\mu _1} \\ \Rightarrow \quad \sin \theta=\frac{\mu _2}{\mu _1} \cdot \cos C=\frac{\mu _2}{\mu _1} \sqrt{1-\sin ^{2} C} \quad \text { [from Eq. (i)] } \\ =\frac{\mu _2}{\mu _1} \sqrt{1-\frac{\mu _1^{2}}{\mu _2^{2}}}=\sqrt{\frac{\mu _2^{2}}{\mu _1^{2}}-1} \Rightarrow \theta=\sin ^{-1} \sqrt{\frac{\mu _2^{2}}{\mu _1^{2}}-1} \end{gathered} $$
For TIR at $E, i>C$
$$ \Rightarrow \quad \theta<\sin ^{-1} \sqrt{\frac{\mu _2^{2}}{\mu _1^{2}}-1} $$






