Optics 1 Question 3
3. A point source of light, $S$ is placed at a distance $L$ in front of the centre of plane mirror of width $d$ which is hanging vertically on a wall. A man walks in front of the mirror along a line parallel to the mirror, at a distance $2 L$ as shown below. The distance over which the man can see the image of the light source in the mirror is
(2019 Main, 12 Jan I)
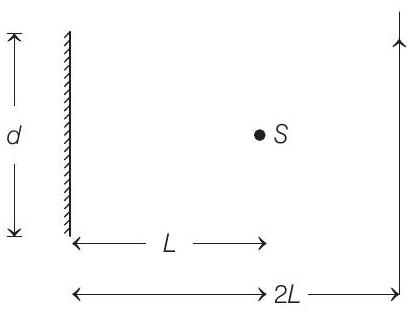
(a) $\frac{d}{2}$
(b) $d$
(c) $3 d$
(d) $2 d$
Show Answer
Answer:
Correct Answer: 3. (c)
Solution:
- Light from mirror is reflected in a straight line and It is appear to come from its image formed at same distance (as that of source) behind the mirror as shown in the ray diagram below.
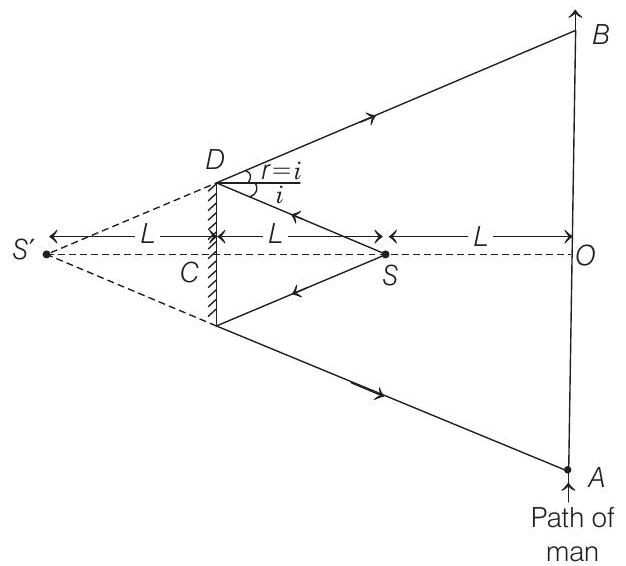
From ray diagram in similar triangles,
$\triangle S^{\prime} C D$ and $\triangle S^{\prime} O B$, we have
$$ \frac{S^{\prime} C}{S^{\prime} O}=\frac{C D}{O B} $$
So, $\quad O B=\frac{C D \times S^{\prime} O}{S^{\prime} C}=\frac{\frac{d}{2} \times 3 L}{L}=\frac{3 d}{2}$
Also, $O A=\frac{3 d}{2}$
So, distance over which man can see the image $S^{\prime}$ is
$$ \frac{3 d}{2}+\frac{3 d}{2}=3 d $$






