SATHEE: Modern Physics 2 Question 1

Modern Physics 2 Question 1

1. The stopping potential $V_{0}$ (in volt) as a function of frequency (v) for a sodium emitter, is shown in the figure. The work function of sodium, from the data plotted in the figure, will be

(Take, Planck’s constant $(h) = 6.63 \times 10^{- 34} J$ -s, electron charge, $e = 1.6 \times 10^{- 19} C$ ]

(Main 2019, 12 April I)

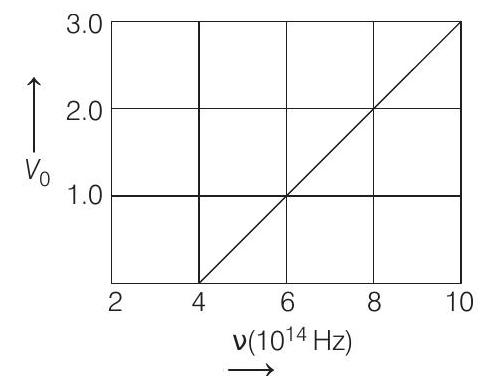
(a) $1.82 e V$

(b) $1.66 e V$

(d) $2.12 e V$

Show Answer

Answer:

Correct Answer: 1. (b)

Solution:

Given,

Planck’s constant,

$\begin{aligned} h & = 6.63 \times 10^{- 34} J - s \\ e & = 1.6 \times 10^{- 19} C \end{aligned}$

and there is a graph between stopping potential and frequency.

We need to determine work function $W$ .

Using Einstein’s relation of photoelectric effect,

$\begin{aligned} (K E)_{max} & = e V_{0} = h ν - h v_{0} = h ν - W [∵ W = h v_{0}] \\ V_{0} & = \frac{h}{e} ν - \frac{W}{e} \end{aligned}$

From graph at $V_{0} = 0$ and $v = 4 \times 10^{14} H z$

$\begin{aligned} ∴ & 0 & = \frac{6.63 \times 10^{- 34}}{e} \times 4 \times 10^{14} - \frac{W}{e} \\ \Rightarrow & \frac{W}{e} & = \frac{6.63 \times 10^{- 34} \times 4 \times 10^{14}}{e} J \end{aligned}$

$\begin{aligned} or & W & = 6.63 \times 4 \times 10^{- 20} J \\ or & W & = \frac{6.63 \times 4 \times 10^{- 20}}{1.6 \times 10^{- 19}} e V = 1.657 e V \\ ∴ & W & = 1.66 e V \end{aligned}$

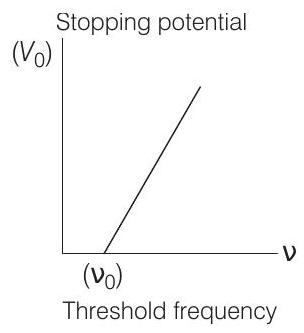
Alternate Solution

From graph, threshold frequency,

$v_{0} = 4 \times 10^{14} H z (where, V_{0} = 0)$

$∴$ Work function, $W = h v_{0}$

$\begin{array}{ll} \Rightarrow & W = 6.63 \times 10^{- 34} \times 4 \times 10^{14} J \\ \Rightarrow & W = \frac{6.63 \times 4 \times 10^{- 20}}{1.6 \times 10^{- 19}} e V = 1.657 e V \approx 1.66 e V \end{array}$

Modern Physics 2 Question 1

1. The stopping potential $V_{0}$ (in volt) as a function of frequency (v) for a sodium emitter, is shown in the figure. The work function of sodium, from the data plotted in the figure, will be

Answer:

Alternate Solution

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Modern Physics 2 Question 1

1. The stopping potential V0 (in volt) as a function of frequency (v) for a sodium emitter, is shown in the figure. The work function of sodium, from the data plotted in the figure, will be

Answer:

Alternate Solution

Engineering Preparation

Medical Preparation

NCERT Books & Solutions

Important Resources

Other Resources

Syllabus

Test Platform

Sample Mock Test

Mentorship

NCERT Exercise Video Solution

Menu

1. The stopping potential $V_{0}$ (in volt) as a function of frequency (v) for a sodium emitter, is shown in the figure. The work function of sodium, from the data plotted in the figure, will be