Magnetics 6 Question 27
30. A rectangular loop $P Q R S$ made from a uniform wire has length $a$, width $b$ and mass $m$. It is free to rotate about the arm $P Q$, which remains hinged along a horizontal line taken as the $y$-axis (see figure). Take the vertically upward direction as the $z$-axis.
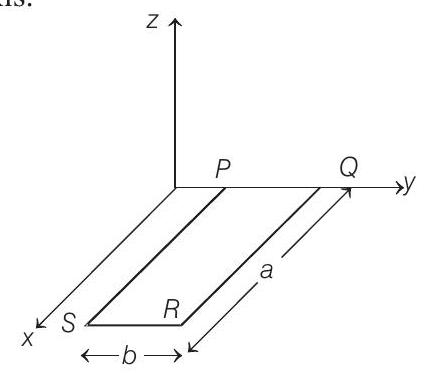
A uniform magnetic field $\mathbf{B}=(3 \hat{\mathbf{i}}+4 \hat{\mathbf{k}}) B _0$ exists in the region. The loop is held in the $x-y$ plane and a current $I$ is passed through it. The loop is now released and is found to stay in the horizontal position in equilibrium.
(2002, 5M)
(a) What is the direction of the current $I$ in $P Q$ ?
(b) Find the magnetic force on the arm $R S$.
(c) Find the expression for $I$ in terms of $B _0, a, b$ and $m$.
Show Answer
Answer:
Correct Answer: 30. (a) $P$ to $Q$ (b) $I b B _0(3 \hat{\mathbf{k}}-4 \hat{\mathbf{i}})$ (c) $\frac{m g}{6 b B _0}$
Solution:
- Let the direction of current in wire $P Q$ is from $P$ to $Q$ and its magnitude be $I$.
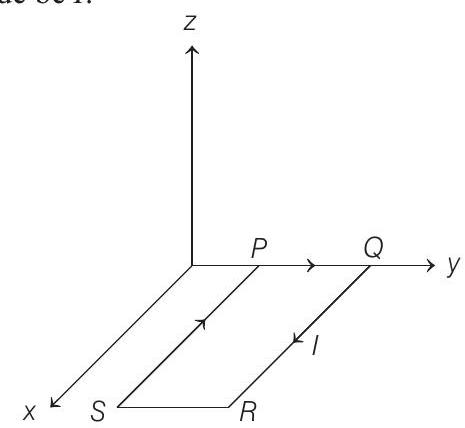
The magnetic moment of the given loop is
$$ \mathbf{M}=-I a b \hat{\mathbf{k}} $$
Torque on the loop due to magnetic forces is
$\tau _1=\mathbf{M} \times \mathbf{B}=(-I a b \hat{\mathbf{k}}) \times(3 \hat{\mathbf{i}}+4 \hat{\mathbf{k}}) B _0 \hat{\mathbf{i}}=-3 \operatorname{Iab} B _0 \hat{\mathbf{j}}$
Torque of weight of the loop about axis $P Q$ is
$$ \tau _2=\mathbf{r} \times \mathbf{F}=\frac{a}{2} \hat{\mathbf{i}} \times(-m g \hat{\mathbf{k}})=\frac{m g a}{2} \hat{\mathbf{j}} $$
We see that when the current in the wire $P Q$ is from $P$ to $Q, \tau _1$ and $\tau _2$ are in opposite directions, so they can cancel each other and the loop may remain in equilibrium. So, the direction of current $I$ in wire $P Q$ is from $P$ to $Q$. Further for equilibrium of the loop
or
$$ \begin{aligned} \left|\tau _1\right| & =\left|\tau _2\right| \\ 3 I a b B _0 & =\frac{m g a}{2} \\ I & =\frac{m g}{6 b B _0} \end{aligned} $$
(b) Magnetic force on wire $R S$ is
$$ \begin{aligned} & \mathbf{F}=I(\mathbf{I} \times \mathbf{B})=I\left[(-b \hat{\mathbf{j}}) \times{(3 \hat{\mathbf{i}}+4 \hat{\mathbf{k}}) B _0 }\right] \\ & \mathbf{F}=I b B _0(3 \hat{\mathbf{k}}-4 \hat{\mathbf{i}}) \end{aligned} $$






