Magnetics 6 Question 2
2. A galvanometer of resistance $100 \Omega$ has 50 divisions on its scale and has sensitivity of $20 \mu A /$ division. It is to be converted to a voltmeter with three ranges of $0-2 V, 0-10 V$ and $0-20 V$. The appropriate circuit to do so is
(a)
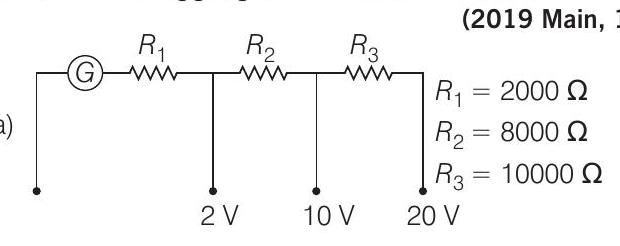
(b)
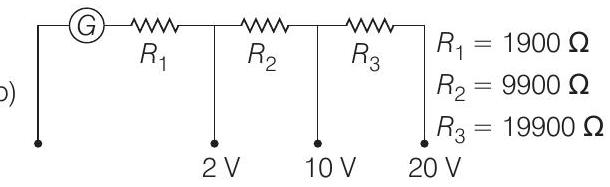
(c)
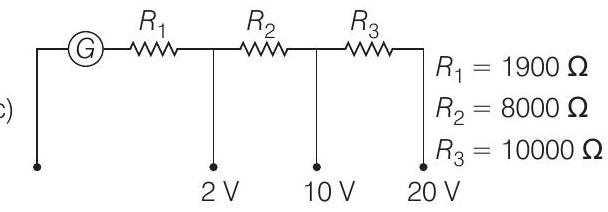
(d)
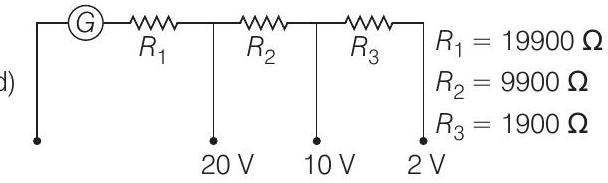
Show Answer
Solution:
- Given, divisions in scale of galvanometer, $n=50$ Sensitivity of galvanometer,
$$ \frac{I _g}{n}=20 \mu A / \text { division } $$
$\therefore$ Current in galvanometer,
$$ \begin{aligned} & I _g=\frac{I _g}{n} \times n=20 \mu A \times 50 \\ & \Rightarrow \quad I _g=1000 \mu A=1 mA \end{aligned} $$
Now, for $R$, it should be converted into $2 V$ voltmeter.
$$ \begin{aligned} & \therefore & V _1 & =I _g\left(R _1+G\right) \\ & & 2 & =10^{-3}\left(R _1+100\right) \\ & \therefore & 2000 & =R _1+100 \\ & & R _1 & =1900 \Omega \end{aligned} $$
For $R _2$, it should be converted into $10 V$ voltmeter.
$$ \begin{aligned} & \therefore \quad V _2=I _g\left[\left(R _1+R _2\right)+G\right] \\ & \Rightarrow \quad 10=10^{-3}\left[\left(R _1+R _2\right)+100\right] \\ & \Rightarrow \quad 10000=R _1+R _2+100=2000+R _2 \\ & \therefore \quad R _2=8000 \Omega \end{aligned} $$
For $R _3$, it should be converted into $20 V$ voltmeter.
$$ \begin{array}{ll} \therefore & V _3=I _g\left[\left(R _1+R _2+R _3+G\right]\right. \\ \Rightarrow & 20=10^{-3}\left[1900+8000+R _3+100\right] \end{array} $$
$$ \begin{array}{llrl} \Rightarrow & & 20000 & =R _3+10000 \\ & \therefore & R _3 & =10000 \Omega \end{array} $$
From Eqs. (i), (ii) and (iii), it is clear that option (c) is correct.






