Magnetics 6 Question 18
18. In the $x y$-plane, the region $y>0$ has a uniform magnetic field $B _1 \hat{k}$ and the region
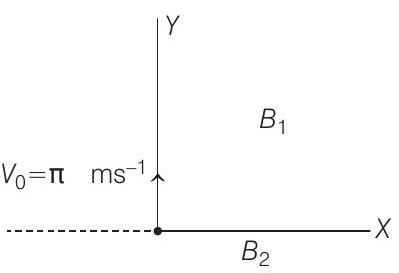 $y<0$ has another uniform magnetic field $B _2 \hat{k}$. A positively charged particle is projected from the origin along the positive $Y$-axis with speed $v _0=\pi ms^{-1}$ at $t=0$, as shown in figure. Neglect gravity in this problem. Let $t=T$ be the time when the particle crosses the $X$-axis from below for the first time. If $B _2=4 B _1$, the average speed of the particle, in $ms^{-1}$, along the $X$-axis in the time interval $T$ is.
$y<0$ has another uniform magnetic field $B _2 \hat{k}$. A positively charged particle is projected from the origin along the positive $Y$-axis with speed $v _0=\pi ms^{-1}$ at $t=0$, as shown in figure. Neglect gravity in this problem. Let $t=T$ be the time when the particle crosses the $X$-axis from below for the first time. If $B _2=4 B _1$, the average speed of the particle, in $ms^{-1}$, along the $X$-axis in the time interval $T$ is.
(2018 Adv.)
Passage Based Questions
Passage 1
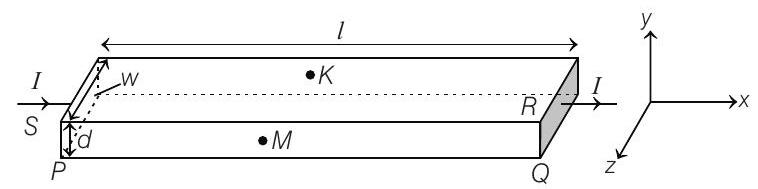
In a thin rectangular metallic strip a constant current $I$ flows along the positive $x$-direction, as shown in the figure. The length, width and thickness of the strip are $l, w$ and $d$, respectively. A uniform magnetic field $\mathbf{B}$ is applied on the strip along the positive $y$-direction. Due to this, the charge carriers experience a net deflection along the $z$-direction.
This results in accumulation of charge carriers on the surface $P Q R S$ and appearance of equal and opposite charges on the face opposite to $P Q R S$. A potential difference along the $z$-direction is thus developed. Charge accumulation continues until the magnetic force is balanced by the electric force. The current is assumed to be uniformly distributed on the cross section of the strip and carried by electrons.
Show Answer
Solution:
- If average speed is considered along $x$-axis,
$$ \begin{gathered} R _1=\frac{m v _0}{q B _1}, R _2=\frac{m v _0}{q B _2}=\frac{m v _0}{4 q B _1} \\ R _1>R _2 \end{gathered} $$
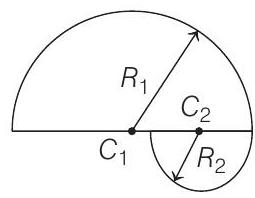
Distance travelled along $x$-axis, $\Delta x=2\left(R _1+R _2\right)=\frac{5 m v _0}{2 q B _1}$ Total time $=\frac{T _1}{2}+\frac{T _2}{2}=\frac{\pi m}{q B _1}+\frac{\pi m}{q B _2}$
$$ =\frac{\pi m}{q B _1}+\frac{\pi m}{4 q B _1}=\frac{5 \pi m}{4 q B _1} $$
Magnitude of average speed $=\frac{\frac{5 m v _0}{2 q B _1}}{\frac{5 \pi m}{4 q B _1}}=2$






