Magnetics 4 Question 3
4. An infinitely long current-carrying wire and a small current-carrying loop are in the plane of the paper as shown. The radius of the loop is $a$ and distance of its centre from the wire is $d(d \gg a)$. If the loop applies a force $F$ on the wire, then
(2019 Main, 9 Jan I)
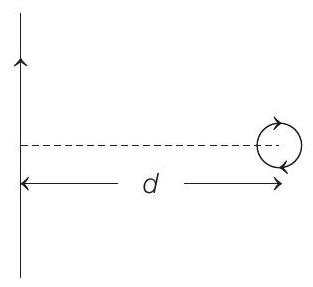
(a) $F \propto \frac{a^{2}}{d^{3}}$
(b) $F=0$
(c) $F \propto \frac{a}{d}$
(d) $F \propto \frac{a}{d}^{2}$
Show Answer
Answer:
Correct Answer: 4. (d)
Solution:
- In the given condition, the current-carrying loop is at a very large distance from the long current-carrying conducting wire. Thus, it can be considered as a dipole (a magnet with north pole facing in upward direction and south in the downward direction). Suppose the effective length of this dipole be ’ $l$ ‘. Thus, the top view of the condition can be shown in the figure given below.
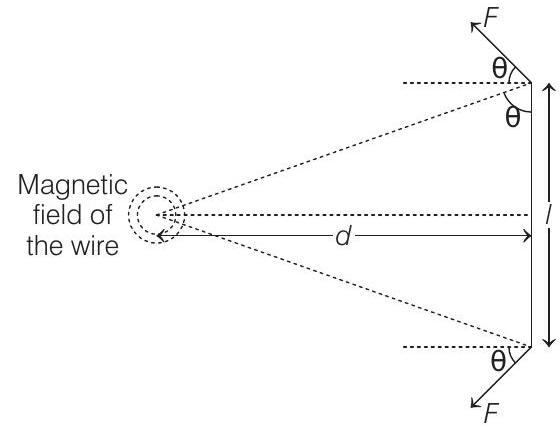
Now, the net force on the loop (i.e. at the two poles) due to the wire is given as,
$$ F _{net}=2 F \cos \theta=2 m B \cos \theta $$
where, $m$ is the pole strength.
From the figure, we have
$$ \begin{aligned} \cos \theta & =\frac{\frac{l}{2}}{\sqrt{d^{2}+\frac{l^{2}}{4}}} \\ \Rightarrow \quad F _{\text {net }} & =\frac{2 m B l}{2 \sqrt{d^{2}+\frac{l^{2}}{4}}} \end{aligned} $$
Since, the magnetic moment of a loop of radius $r$ is
$$ M=I A=I \pi r^{2}=m l $$
and magnetic field due to a straight infinitely long current-carrying conductor at a distance $x$ is
$$ B=\frac{\mu _0 I^{\prime}}{2 \pi x} $$
$\therefore$ Using Eqs. (ii) and (iii), rewriting Eq. (i), we get
$$ \begin{aligned} & F _{\text {net }}=\frac{I \pi a^{2} \mu _0 I^{\prime}}{2 \pi \sqrt{d^{2}+\frac{l^{2}}{4}}} \\ & \Rightarrow \quad F _{\text {net }} \propto \frac{a^{2}}{d^{2}+\frac{l^{2}}{4}} \end{aligned} $$
$l$ can be neglected as the loop is kept at very large distance.
$$ \text { or } \quad F _{\text {net }} \propto \frac{a}{d}^{2} $$






