Magnetics 4 Question 2
3. An insulating thin rod of length $l$ has a linear charge density $\rho(x)=\rho _0 \frac{x}{l}$ on it. The rod is rotated about an axis passing through the origin $(x=0)$ and perpendicular to the rod. If the rod makes $n$ rotations per second, then the time averaged magnetic moment of the rod is
(2019 Main, 10 Jan I)
(a) $n \rho l^{3}$
(b) $\pi n \rho l^{3}$
(c) $\frac{\pi}{3} n \rho l^{3}$
(d) $\frac{\pi}{4} n \rho l^{3}$
Show Answer
Answer:
Correct Answer: 3. (d)
Solution:
$$ \begin{aligned} & \left(R _2=\right.\text { radius of coil } \\ & \text { having } N \text { loops) } \end{aligned} $$
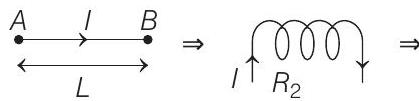
Key Idea A rotating charge constitutes a current. Hence, a rotating charged rod behaves like a current carrying coil. If charge q rotates with a frequency $n$, then equivalent current is $I=q n \quad$ and magnetic moment associated with this current is $M=I A$
where, $A$ =area of coil or area swept by rotating rod. Let $d q$ be the charge on $d x$ length of rod at a distance $x$ from origin as shown in the figure below.
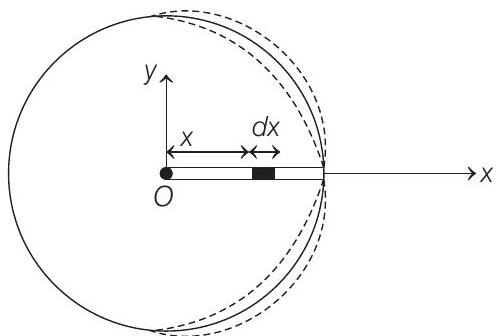
The magnetic moment $d m$ of this portion $d x$ is given as
$$ \begin{aligned} d m & =(d I) A \\ d m & =n d q A \quad[\because I=q n, \therefore d I=n \cdot d q] \\ & =n \rho d x A \end{aligned} $$
where, $\rho=$ charge density of $\operatorname{rod}=\rho _0 \frac{x}{l}$.
So, $\quad d m=\frac{n \rho _0 x d x \pi x^{2}}{l}=\frac{\pi n \rho _0}{l} \cdot x^{3} \cdot d x$
Total magnetic moment associated with rotating rod is sum of all the magnetic moments of such differentiable elements of rod.
So, magnetic moment associated with complete rod is
$$ \begin{aligned} M & =\int _{x=0}^{x=l} d m \\ & =\int _0^{l} \frac{\pi n \rho _0}{l} \cdot x^{3} d x=\frac{\pi n \rho _0}{l} \cdot \int _0^{l} x^{3} d x \\ & =\frac{\pi n \rho _0}{l} \frac{x^{4}}{4}=\frac{\pi n \rho _0 l^{3}}{4} \end{aligned} $$
$$ \begin{array}{rlrl} \text { at } & & x & =l \\ \rho & =\rho _0 \\ \therefore & M & =\frac{\pi}{4} n \rho l^{3} \end{array} $$
