Magnetics 4 Question 16
17. A uniform constant magnetic field $\mathbf{B}$ is directed at an angle of $45^{\circ}$ to the $x$-axis in $x-y$ plane. $P Q R S$ is rigid square wire frame carrying a steady current $I _0$, with its centre at the origin $O$. At time $t=0$, the frame is at rest in the position shown in the figure with its sides parallel to $x$ and $y$-axes. Each side of the frame is of mass $M$ and length $L$
$(1998,8$ M)
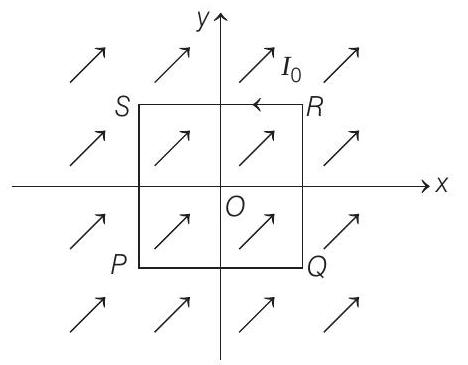
(a) What is the magnitude of torque $\tau$ acting on the frame due to the magnetic field?
(b) Find the angle by which the frame rotates under the action of this torque in a short interval of time $\Delta t$ and the axis about which this rotation occurs ( $\Delta t$ is so short that any variation in the torque during this interval may be neglected). Given : the moment of inertia of the frame about an axis through its centre perpendicular to its plane is $\frac{4}{3} M L^{2}$.
Show Answer
Answer:
Correct Answer: 17. (a) $|\tau|=I _0 L^{2} B$ (b) $\theta=\frac{3}{4} \frac{I _0 B}{M}(\Delta t)^{2}$
Solution:
- Magnetic moment of the loop, $\mathbf{M}=(i A) \hat{\mathbf{k}}=\left(I _0 L^{2}\right) \hat{\mathbf{k}}$ Magnetic field, $\mathbf{B}=\left(B \cos 45^{\circ}\right) \hat{\mathbf{i}}+\left(B \sin 45^{\circ}\right) \hat{\mathbf{j}}$
$$ =\frac{B}{\sqrt{2}}(\hat{\mathbf{i}}+\hat{\mathbf{j}}) $$
(a) Torque acting on the loop, $\tau=\mathbf{M} \times \mathbf{B}$
$$ \begin{array}{rlrl} & =\left(I _0 L^{2} \hat{\mathbf{k}}\right) \times \frac{B}{\sqrt{2}}(\hat{\mathbf{i}}+\hat{\mathbf{j}}) \\ \therefore & \tau & =\frac{I _0 L^{2} B}{\sqrt{2}}(\hat{\mathbf{j}}-\hat{\mathbf{i}}) \\ \text { or } & & |\tau| l=I _0 L^{2} B \end{array} $$
(b) Axis of rotation coincides with the torque and since torque is in $\hat{\mathbf{j}}-\hat{\mathbf{i}}$ direction or parallel to $Q S$. Therefore, the loop will rotate about an axis passing through $Q$ and $S$ as shown in the figure.
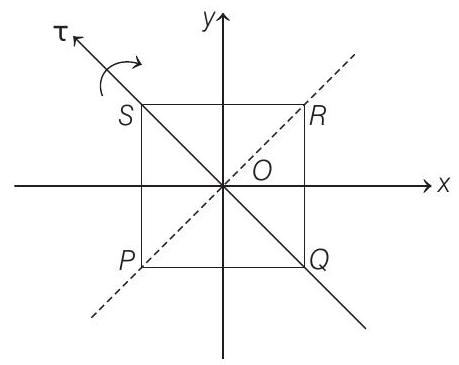
Angular acceleration, $\alpha=\frac{|\tau|}{I}$
where, $I=$ moment of inertia of loop about $Q S$.
$$ I _{Q S}+I _{P R}=I _{Z Z} $$
(From theorem of perpendicular axis)
$$ \begin{array}{rlrl} \text { But } & I _{Q S} & =I _{P R} \\ \therefore & 2 I _{Q S} & =I _{Z Z}=\frac{4}{3} M L^{2} \\ & \therefore & I _{Q S} & =\frac{2}{3} M L^{2} \\ & \alpha & =\frac{|\tau|}{I}=\frac{I _0 L^{2} B}{2 / 3 M L^{2}}=\frac{3}{2} \frac{I _0 B}{M} \end{array} $$
$\therefore$ Angle by which the frame rotates in time $\Delta t$ is
$$ \theta=\frac{1}{2} \alpha(\Delta t)^{2} \text { or } \theta=\frac{3}{4} \frac{I _0 B}{M} \cdot(\Delta t)^{2} $$






