Magnetics 2 Question 19
19. A cylindrical cavity of diameter $a$ exists inside a cylinder of diameter $2 a$ as shown in the figure. Both the cylinder and the cavity are infinitely long. A uniform current density $J$ flows along the length. If the magnitude of the magnetic field at the point $P$ is given by $\frac{N}{12} \mu _0 a J$, then the value of $N$ is
(2012)
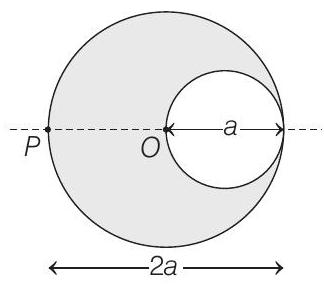
Show Answer
Answer:
Correct Answer: 19. 5
Solution:
- $B _R=B _T-B _C$
$R=$ Remaining portion
$T=$ Total portion and
$C=$ Cavity
$$ \begin{aligned} B _R & =\frac{\mu _0 I _T}{2 a \pi}-\frac{\mu _0 I _C}{2(3 a / 2) \pi} \\ I _T & =J\left(\pi a^{2}\right) \\ I _C & =J \frac{\pi a^{2}}{4} \end{aligned} $$
Substituting the values in Eq. (i), we have
$$ \begin{aligned} B _R & =\frac{\mu _0}{a \pi} \frac{I _T}{2}-\frac{I _C}{3} \\ & =\frac{\mu _0}{a \pi} \frac{\pi a^{2} J}{2}-\frac{\pi a^{2} J}{12}=\frac{5 \mu _0 a J}{12} \\ \therefore \quad N & =5 \end{aligned} $$






