Magnetics 1 Question 36
36. A particle of mass $m=1.6 \times 10^{-27} kg$ and charge $q=1.6 \times 10^{-19} C$ enters a region of uniform magnetic field of strength $1 T$ along the direction shown in figure. The speed of the particle is $10^{7} m / s$.
$(1984,8$ M)
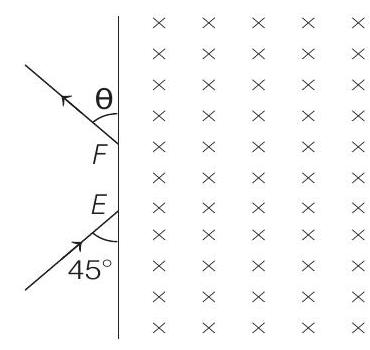
(a) The magnetic field is directed along the inward normal to the plane of the paper. The particle leaves the region of the field at the point $F$. Find the distance $E F$ and the angle $\theta$.
(b) If the direction of the field is along the outward normal to the plane of the paper, find the time spent by the particle in the region of the magnetic field after entering it at $E$.
Show Answer
Answer:
Correct Answer: 36. $1.2 \times 10^{-2} m, 4.37 \times 10^{-2} m$
Solution:
- Inside a magnetic field speed of charged particle does not change. Further, velocity is perpendicular to magnetic field in both the cases hence path of the particle in the magnetic field will be circular. Centre of circle can be obtained by drawing perpendiculars to velocity (or tangent to the circular path) at $E$ and $F$. Radius and angular speed of circular path would be
and
$$ r=\frac{m v}{B q} $$
$$ \omega=\frac{B q}{m} $$
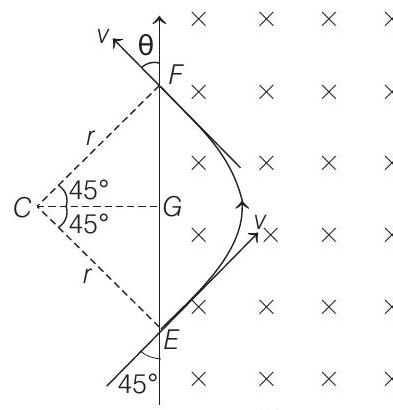
(i)
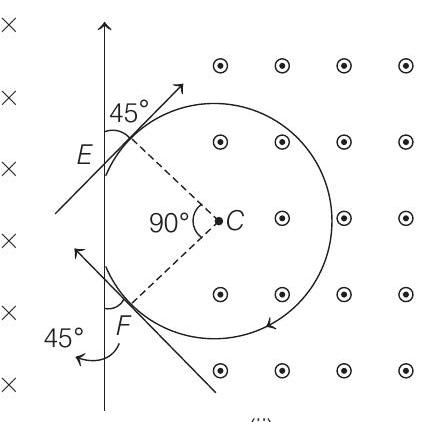
(ii)
(a) Refer figure (i)
$$ \begin{aligned} & \angle C F G=90^{\circ}-\theta \text { and } \angle C E G=90^{\circ}-45^{\circ}=45^{\circ} \\ & \text { Since, } \quad C F=C E \\ & \therefore \quad \angle C F G=\angle C E G \\ & \text { or } \quad 90^{\circ}-\theta=45^{\circ} \quad \text { or } \theta=45^{\circ} \\ & \text { Further, } \quad F G=G E=r \cos 45^{\circ} \\ & \therefore E F=2 F G=2 r \cos 45^{\circ}=\frac{2 m v \cos 45^{\circ}}{B q} \\ & \qquad=\frac{2\left(1.6 \times 10^{-27}\right)\left(10^{7}\right) \frac{1}{\sqrt{2}}}{(1)\left(1.6 \times 10^{-19}\right)}=0.14 m \end{aligned} $$
NOTE That in this case particle completes $1 /$ th of circle in the magnetic field.
(b) Refer figure (ii) In this case particle will complete
$\frac{3}{4}$ th of circle in the magnetic field. Hence, the time spent in the magnetic field
$$ \begin{aligned} t & =\frac{3}{4} \\ & =\frac{3}{4} \frac{2 \pi m}{B q}=\frac{3 \pi m}{2 B q} \\ & =\frac{(3 \pi)\left(1.6 \times 10^{-27}\right)}{(2)(1)\left(1.6 \times 10^{-19}\right)} \\ & =4.712 \times 10^{-8} s \end{aligned} $$
( time period of circular motion)






