Laws of Motion 5 Question 1
1. Two forces $P$ and $Q$ of magnitude $2 F$ and $3 F$, respectively are at an angle $\theta$ with each other. If the force $Q$ is doubled, then their resultant also gets doubled. Then, the angle $\theta$ is
(a) $60^{\circ}$
(b) $120^{\circ}$
(c) $30^{\circ}$
(d) $90^{\circ}$
Show Answer
Answer:
Correct Answer: 1. (b)
Solution:
- Resultant force $\mathbf{F}_ {r}$ of any two forces $\mathbf{F}_ {1}$ (i.e. $P$ ) and $\mathbf{F}_ {2}$ (i.e. $Q$ ) with an angle $\theta$ between them can be given by vector addition as
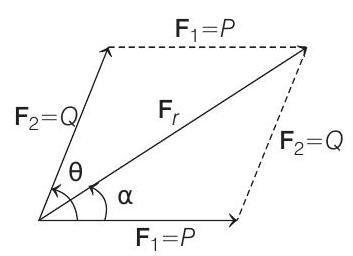
In first case $F_{1}=2 F$ and $F_{2}=3 F$
$$ \begin{array}{ll} \Rightarrow & F_{r}^{2}=4 F^{2}+9 F^{2}+2 \times 2 \times 3 F^{2} \cos \theta \\ \Rightarrow & F_{r}^{2}=13 F^{2}+12 F^{2} \cos \theta \quad \cdots(ii) \end{array} $$
In second case $F_{1}=2 F$ and $F_{2}=6 F \quad$ $(\because$ Force $Q$ gets doubled)
$$ \text { and } \quad F_{r}^{\prime}=2 F_{r} \quad (Given) $$
By putting these values in Eq. (i), we get
$$ \begin{aligned} \left(2 F_{r}\right)^{2} & =(2 F)^{2}+(6 F)^{2}+2 \times 2 \times 6 F^{2} \cos \theta \\ \Rightarrow \quad 4 F_{r}^{2} & =40 F^{2}+24 F^{2} \cos \theta \quad \cdots(iii) \end{aligned} $$
From Eq. (ii) and Eq. (iii), we get;
$$ \begin{aligned} & 52 F^{2}+48 F^{2} \cos \theta=40 F^{2}+24 F^{2} \cos \theta \\ \Rightarrow \quad & 12+24 \cos \theta=0 \text { or } \cos \theta=-1 / 2 \\ \text { or } & \theta=120^{\circ} \quad\left(\because \cos 120^{\circ}=-1 / 2\right) \end{aligned} $$
