Laws of Motion 3 Question 7
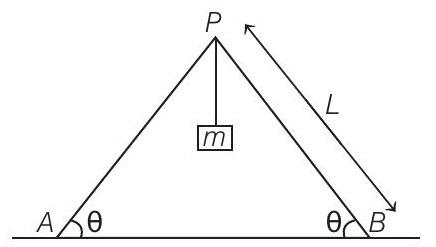
7. Two identical ladders are arranged as shown in the figure. Mass of each ladder is $M$ and length $L$. The system is in equilibrium. Find direction and magnitude of frictional force acting at $A$ or $B$.
(2005)
Show Answer
Answer:
Correct Answer: 7. (a)
Solution:
- A block of mass $m$ is placed on a surface with a vertical cross-section, then
$$ \tan \theta=\frac{d y}{d x} \frac{d \frac{x^{3}}{6}}{d x}=\frac{x^{2}}{2} $$
At limiting equilibrium, we get
$$ \begin{array}{rlrl} \mu & =\tan \theta \\ \Rightarrow & & 0.5 & =\frac{x^{2}}{2} \\ \Rightarrow & x^{2} & =1 \\ & x & = \pm 1 \end{array} $$
Now, putting the value of $x$ in $y=\frac{x^{3}}{6}$, we get
$$ \begin{array}{l|l} \text { When } x=1 & \text { When } x=-1 \\ y=\frac{(1)^{3}}{6}=\frac{1}{6} & y=\frac{(-1)^{3}}{6}=\frac{-1}{6} \end{array} $$
So, the maximum height above the ground at which the block can be placed without slipping is $1 / 6 m$.
