Laws of Motion 3 Question 6
6. In the figure, a ladder of mass
(2014 Adv.)
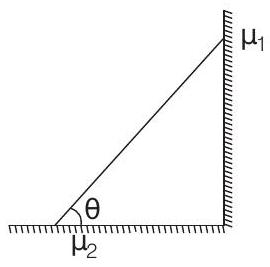
(a)
(b)
(c)
(d)
Show Answer
Answer:
Correct Answer: 6. (b)
Solution:
- NOTE
It is not given in the question, best assuming that both blocks are in equilibrium. The free body diagram of two blocks is as shown below,
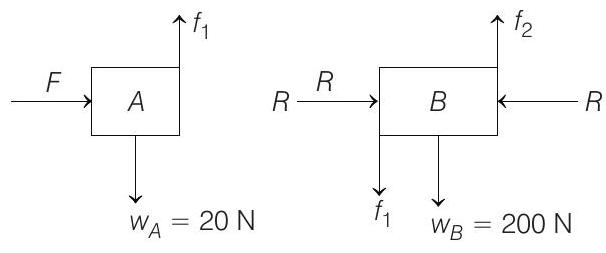
Reaction force,
For vertical equilibrium of
For vertical equilibrium of






