Laws of Motion 3 Question 24
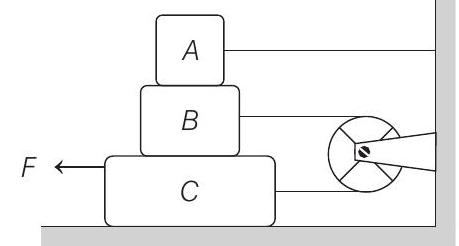
26. In the figure, the blocks $A, B$ and $C$ have masses $3 \mathrm{~kg}, 4 \mathrm{~kg}$ and $8 \mathrm{~kg}$ respectively. The coefficient of sliding friction between any two surfaces is $0.25 . A$ is held at rest by a massless rigid rod fixed to the wall, while $B$ and $C$ are connected by a light flexible cord passing around a fixed frictionless pulley. Find the force $F$ necessary to drag $C$ along the horizontal surface to the left at a constant speed. Assume that the arrangement shown in the figure. i.e. $B$ on $C$ and $A$ on $B$, is maintained throughout.(Take $g=10 \mathrm{~m} / \mathrm{s}^{2}$ ).
(1978)
Show Answer
Answer:
Correct Answer: 26. $80 \mathrm{~N}$
Solution:
- Maximum friction between $A$ and $B=\mu m_{A} g$
or
$$ f_{1}=0.25(3)(10)=7.5 \mathrm{~N} $$
Maximum friction between $B$ and $C=\mu\left(m_{A}+m_{B}\right) g$
or
$$ \begin{aligned} f_{2} & =0.25(3+4)(10) \\ & =17.5 \mathrm{~N} \end{aligned} $$
Maximum friction between $C$ and ground
$$ \begin{aligned} f_{3} & =\mu\left(m_{A}+m_{B}+m_{C}\right) g \\ & =0.25(3+4+8)(10) \\ & =37.5 \mathrm{~N} \end{aligned} $$
Block $C$ and hence block $B$ are moving in opposite directions with constant velocities and block $A$ is at rest. Hence, net force on all three blocks should be zero.
Free body diagrams have been shown below (Only horizontal forces are shown)
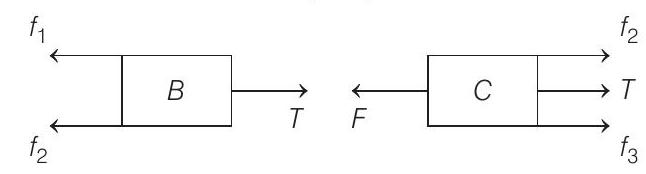
For equilibrium of B$, T=f_{1}+f_{2}=25 \mathrm{~N}$
For equilibrium of C$, F=T+f_{2}+f_{3}=80 \mathrm{~N}$






