Laws of Motion 3 Question 20
21. Block $A$ of mass $m$ and block $B$ of mass $2 m$ are placed on a fixed triangular wedge by means of a massless, in extensible string and a frictionless pulley as shown in figure. The wedge is inclined at $45^{\circ}$ to the horizontal on both sides. The coefficient of friction between block $A$ and the wedge is $2 / 3$ and that between block $B$ and the wedge is $1 / 3$. If the blocks $A$ and $B$ are released from rest, find
(1997C, 5M)
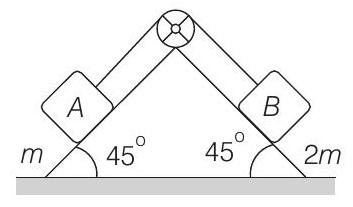
(a) the acceleration of $A$,
(b) tension in the string and
(c) the magnitude and direction of the force of friction acting on $A$.
Show Answer
Answer:
Correct Answer: 21. (a) acceleration $=0 \quad$ (b) $\frac{2 \sqrt{2}}{3} m g \quad$ (c) $\frac{m g}{3 \sqrt{2}}$ (down the plane)
Solution:
- (a) Acceleration of block $A$
Maximum friction force that can be obtained at $A$ is
$$ (f_ {\max })_ {A}=\mu_ {A}(m g \cos 45^{\circ}) $$
$$ =\frac{2}{3}(m g / \sqrt{2})=\frac{\sqrt{2} m g}{3} $$
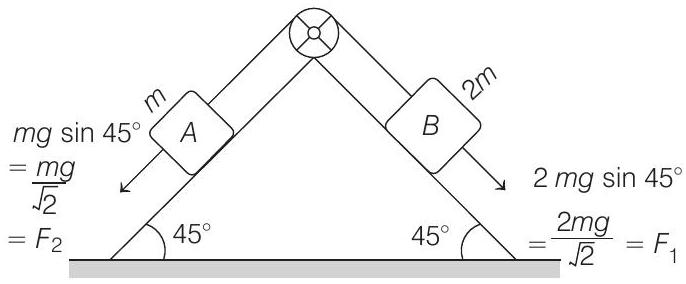
Similarly,
$$ \begin{aligned} (f_ {\max })_ {B} & =\mu_ {B}(2 m g \cos 45^{\circ}) \\ & =\frac{1}{3}(2 m g / \sqrt{2})=\frac{\sqrt{2} m g}{3} \end{aligned} $$
Therefore, maximum value of friction that can be obtained on the system is
$$ (f_ {\max })=(f_ {\max })_ {A}+(f_ {\max })_ {B}=\frac{2 \sqrt{2} m g}{3} \cdots(i) $$
Net pulling force on the system is
$$ F=F_ {1}-F_ {2}=\frac{2 m g}{\sqrt{2}}-\frac{m g}{\sqrt{2}}=\frac{m g}{\sqrt{2}} \cdots(ii) $$
From Eqs. (i) and (ii), we can see that
Net pulling force $<f_ {\max }$. Therefore, the system will not move or the acceleration of block $A$ will be zero.
(b) and (c) Tension in the string and friction at $A$
Net pulling force on the system (block $A$ and $B$ )
$$ F=F_ {1}-F_ {2}=m g / \sqrt{2} $$
Therefore, total friction force on the blocks should also be equal to $\frac{m g}{\sqrt{2}}$
or
$$ f_ {A}+f_ {B}=F=m g / \sqrt{2} $$
Now, since the blocks will start moving from block $B$ first (if they move), therefore, $f_{B}$ will reach its limiting value first and if still some force is needed, it will be provided by $f_{A}$.
Here,
$$ \left(f_{\max }\right)_{B}<F $$
Therefore, $f_{B}$ will be in its limiting value and rest will be provided by $f_{A}$.
Hence, $f_{B}=\left(f_{\max }\right)_{B}=\frac{\sqrt{2} m g}{3}$
and
$$ \begin{aligned} f_{A} & =F-f_{B} \\ & =\frac{m g}{\sqrt{2}}-\frac{\sqrt{2} m g}{3}=\frac{m g}{3 \sqrt{2}} \end{aligned} $$
The FBD of the whole system will be as shown in the figure.
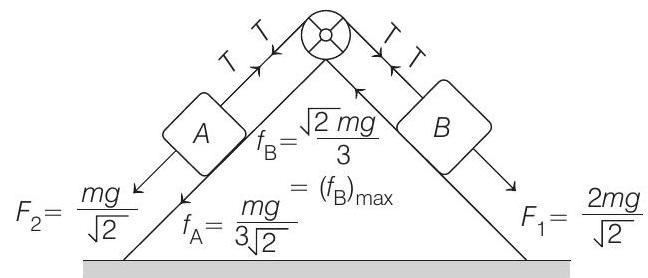
Therefore, friction on $A$ is
$$ f_{A}=m g / 3 \sqrt{2} \quad \text { (down the plane) } $$
Now, for tension $T$ in the string, we may consider either equilibrium of $A$ or $B$.
Equilibrium of $A$ gives
$$ \begin{aligned} T=F_{2}+f_{A} & =\frac{m g}{\sqrt{2}}+\frac{m g}{3 \sqrt{2}}=\frac{4 m g}{3 \sqrt{2}} \\ \text { or } \quad T & =\frac{2 \sqrt{2} m g}{3} \end{aligned} $$
Similarly, equilibrium of $B$ gives $T+f_{B}=F_{1}$
$$ \text { or } \quad \begin{aligned} T & =F_{1}-f_{B} \\ & =\frac{2 m g}{\sqrt{2}}-\frac{\sqrt{2} m g}{3}=\frac{4 m g}{3 \sqrt{2}} \\ \text { or } \quad & =\frac{2 \sqrt{2} m g}{3} \end{aligned} $$
Therefore, tension in the string is $\frac{2 \sqrt{2} m g}{3}$.
