Laws of Motion 2 Question 1
1. A block of mass $5 \mathrm{~kg}$ is (i) pushed in case (A) and (ii) pulled in case (B), by a force $F=20 \mathrm{~N}$, making an angle of $30^{\circ}$ with the horizontal, as shown in the figures. The coefficient of friction between the block, the floor is $\mu=0.2$. The difference between the accelerations of the block, in case (B) and case (A) will be (Take, $g=10 \mathrm{~ms}^{-2}$ )

(A)
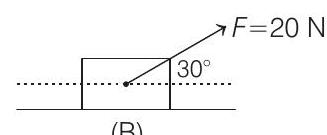
(B)
(a) $0.4 \mathrm{~ms}^{-2}$
(b) $3.2 \mathrm{~ms}^{-2}$
(c) $0.8 \mathrm{~ms}^{-2}$
(d) $0 \mathrm{~ms}^{-2}$
Show Answer
Answer:
Correct Answer: 1. (c)
Solution:
- Case I Block is pushed over surface

Free body diagram of block is

In this case, normal reaction,
$N=m g+F \sin 30^{\circ}=5 \times 10+20 \times \frac{1}{2}=60 \mathrm{~N}$
[Given, $m=5 \mathrm{~kg}, F=20 \mathrm{~N}$ ]
Force of function, $f=\mu \mathrm{N}$
$$ \begin{aligned} & =0.2 \times 60 \quad[\because \mu=0.2] \\ & =12 \mathrm{~N} \end{aligned} $$
So, net force causing acceleration $\left(a_{1}\right)$ is
$$ F_{\text {net }}=m a_{1}=F \cos 30^{\circ}-f $$
$\Rightarrow \quad m a_{1}=20 \times \frac{\sqrt{3}}{2}-12$
$\therefore \quad a_{1}=\frac{10 \sqrt{3}-12}{5} \approx 1 \mathrm{~ms}^{-2}$
Case II Block is pulled over the surface
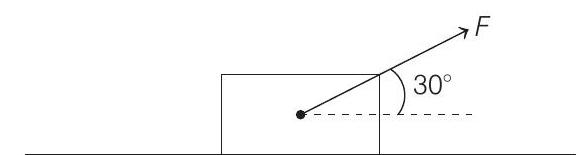
Free body diagram of block is,

Net force causing acceleration is
$$ \begin{aligned} & F_{\text {net }}=F \cos 30^{\circ}-f=F \cos 30^{\circ}-\mu N \\ \Rightarrow \quad & F_{\text {net }}=F \cos 30^{\circ}-\mu\left(m g-F \sin 30^{\circ}\right) \end{aligned} $$
If acceleration is now $a_{2}$, then
$$ \begin{aligned} & a_{2}=\frac{F_{\text {net }}}{m}=\frac{F \cos 30^{\circ}-\mu\left(m g-F \sin 30^{\circ}\right)}{m} \\ & =\frac{20 \times \frac{\sqrt{3}}{2}-0.2\Big(5 \times 10-20 \times \frac{1}{2}\Big)}{5}=\frac{10 \sqrt{3}-8}{5} \\ \Rightarrow & \mathrm{a}_{2} \approx 1.8 \mathrm{~ms}^{-2} \end{aligned} $$
So, difference $=a_{2}-a_{1}=1.8-1=0.8 \mathrm{~ms}^{-2}$






