Kinematics 6 Question 8
8. The coordinates of a particle moving in a plane are given by $x(t)=a \cos (p t)$ and $y(t)=b \sin (p t)$ where $a, b(<a)$ and $p$ are positive constants of appropriate dimensions. Then,
(1999, 3M)
(a) the path of the particle is an ellipse
(b) the velocity and acceleration of the particle are normal to each other at $t=\pi / 2 p$
(c) the acceleration of the particle is always directed towards a focus
(d) the distance travelled by the particle in time interval $t=0$ to $t=\pi / 2 p$ is $a$
Show Answer
Answer:
Correct Answer: 8. $(a, b, c)$
Solution:
- $x=a \cos (p t) \Rightarrow \cos (p t)=\frac{x}{a} \cdots(i)$
$$ \Rightarrow \quad \sin (p t)=y / b \cdots(ii) $$
Squaring and adding Eqs. (i) and (ii), we get
$$ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 $$
Therefore, path of the particle is an ellipse. Hence, option (a) is correct.
From the given equations, we can find
$\frac{d x}{d t}=v _x=-a p \sin$
$\Rightarrow \frac{d^{2} x}{d t^{2}}=a _x=-a p^{2} \cos p t$
$$ \frac{d y}{d t}=v _y=b p \cos p t $$
and $\frac{d^{2} y}{d t^{2}}=a _y=-b p^{2} \sin p t$
At time $t=\pi / 2 p$ or $p t=\pi / 2$
$a _x$ and $v _y$ become zero (because $\cos \pi / 2=0$ ),
only $v _x$ and $a _y$ are left.
or we can say that velocity is along negative $x$-axis and acceleration along $y$-axis.
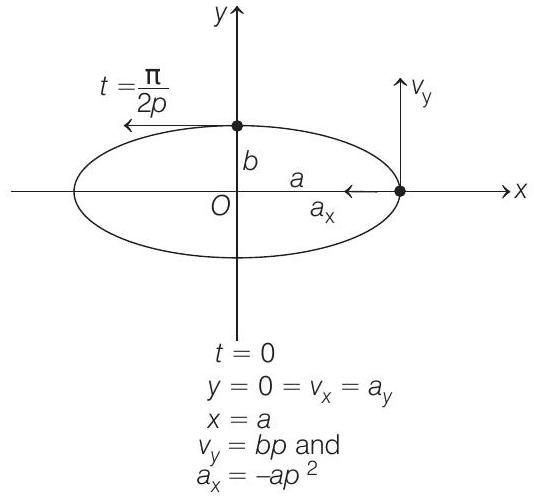
Hence, at $t=\pi / 2 p$ velocity and acceleration of the particle are normal to each other. So, option (b) is also correct.
At $t=t$, position of the particle
$$ \mathbf{r}(t)=x \hat{\mathbf{i}}+y \hat{\mathbf{j}}=a \cos p t \hat{\mathbf{i}}+b \sin p t \hat{\mathbf{j}} $$
and acceleration of the particle is
$$ \begin{aligned} \mathbf{a}(t) & =a _x \hat{\mathbf{i}}+a _y \hat{\mathbf{j}}=-p^{2}[a \cos p t \hat{\mathbf{i}}+b \sin p t \hat{\mathbf{j}}] \\ & =-p^{2}[x \hat{\mathbf{i}}+\mathbf{y} \hat{\mathbf{j}}]=-p^{2} \mathbf{r}(t) \end{aligned} $$
Therefore, acceleration of the particle is always directed towards origin.
Hence, option (c) is also correct.
At $t=0$, particle is at $(a, 0)$ and at $t=\pi / 2 p$
particle is at $(0, b)$. Therefore, the distance covered is one-fourth of the elliptical path not $a$.
Hence, option (d) is wrong.
