Kinematics 6 Question 12
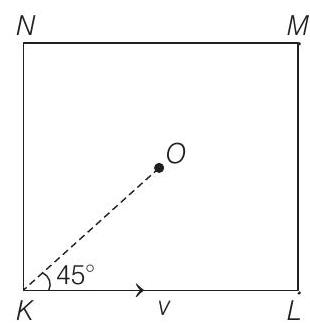
12. Four persons $K, L, M, N$ are initially at the four corners of a square of side $d$. Each person now moves with a uniform speed $v$ in such a way that $K$ always moves directly towards $L, L$ directly towards $M, M$ directly towards $N$ and $N$ directly towards $K$. The four persons will meet at a time
(1984, 2M)
Show Answer
Answer:
Correct Answer: 12. $d / v$
Solution:
- By symmetry, we can say that all will meet at the centre of square.
Component of velocity along $K O$ (or $L O$ etc) at any instant will be $v \cos 45^{\circ}$ or $\frac{v}{\sqrt{2}}$.
Further distance $K O$
$$ =\sqrt{2} \quad \Big(\frac{d}{2}\Big)=\frac{d}{\sqrt{2}} $$
$\therefore \quad$ Time $=\frac{d / \sqrt{2}}{v / \sqrt{2}}=\frac{d}{v}$