Kinematics 5 Question 12
13. An object $A$ is kept fixed at the point $x=3 m$ and $y=1.25 m$ on a plank $P$ raised above the ground. At time $t=0$, the plank starts moving along the $+x$-direction with an acceleration $1.5 m / s^{2}$. At the same instant, a stone is projected from the origin with a velocity $\mathbf{u}$ as shown. A stationary person on the ground observes the stone hitting the object during its downward motion at an angle of $45^{\circ}$ to the horizontal. All the motions are in $x-y$ plane. Find $\mathbf{u}$ and the time after which the stone hits the object. (Take $g=10 m / s^{2}$ ).
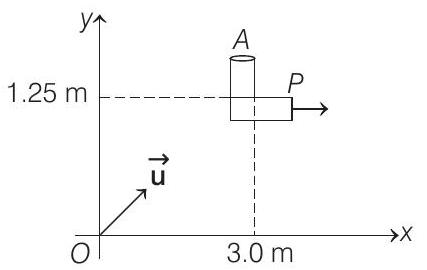
(2000, 10M)
Show Answer
Answer:
Correct Answer: 13. $\mathbf{u}=(3.75 \hat{\mathbf{i}}+6.25 \hat{\mathbf{j}}) m / s, 1 s$
Solution:
- Let $t$ be the time after which the stone hits the object and $\theta$ be the angle which the velocity vector $\mathbf{u}$ makes with horizontal. According to question, we have following three conditions.
Vertical displacement of stone is $1.25 m$.
$$ 1.25=(u \sin \theta) t-\frac{1}{2} g t^2 $$
where,
$$ g=10 \mathrm{~m} / \mathrm{s}^2 $$
or
$$ (u \sin \theta) t=1.25+5 t^2 \cdots(i) $$
Horizontal displacement of stone
$=3+$ displacement of object $A$
$\therefore \quad(u \cos \theta) t=3+\frac{1}{2} a t^2$,
where, $a=1.5 \mathrm{~m} / \mathrm{s}^2$
or $(u \cos \theta) t=3+0.75 t^2 \cdots(ii)$
Horizontal component of velocity (of stone) $=$ vertical component (because velocity vector is inclined at $45^{\circ}$ with horizontal)
$$ \therefore \quad(u \cos \theta)=g t-(u \sin \theta) \cdots(iii) $$
(The right hand side is written $g t-u \sin \theta$ because the stone is in its downward motion. Therefore, $g t>u \sin \theta$. In upward motion $u \sin \theta>g t)$. Multiplying Eq. (iii) with $t$, we can write or $$ (u \cos \theta) t+(u \sin \theta) t=10 t^2 $$
Now Eqs. (iv), (ii) and (i) gives $$ 4.25 t^2-4.25=0 $$ or $$ t=1 \mathrm{~s} $$
Substituting $t=1 \mathrm{~s}$ in Eqs. (i) and (ii), we get $$ \begin{aligned} u \sin \theta & =6.25 \mathrm{~m} / \mathrm{s} \ u_y & =6.25 \mathrm{~m} / \mathrm{s} \ u \cos \theta & =3.75 \mathrm{~m} / \mathrm{s} \end{aligned} $$ or $$ u_y=6.25 \mathrm{~m} / \mathrm{s} $$ and $$ u \cos \theta=3.75 \mathrm{~m} / \mathrm{s} $$ or $$ u_x=3.75 \mathrm{~m} / \mathrm{s} $$
Therefore, $$ \begin{aligned} & \mathbf{u}=u_x \hat{\mathbf{i}}+u_y \hat{\mathbf{j}} \mathrm{m} / \mathrm{s} \ & \mathbf{u}=(3.75 \hat{\mathbf{i}}+6.25 \hat{\mathbf{j}}) \mathrm{m} / \mathrm{s} \end{aligned} $$ or $$ \mathbf{u}=(3.75 \hat{\mathbf{i}}+6.25 \hat{\mathbf{j}}) \mathrm{m} / \mathrm{s} $$
NOTE
Most of the problems of projectile motion are easily solved by breaking the motion of the particle in two suitable mutually perpendicular directions, say $x$ and $y$. Find $u_x, u_y, a_x$ and $\mathrm{a}_{\mathrm{y}}$ and then apply $$ v_x=u_x+a_x t ; s_y=u_y t+\frac{1}{2} a_y t^2 \text { etc. } $$






