Heat and Thermodynamics 6 Question 35
40. Two moles of helium gas $(\gamma=5 / 3)$ are initially at temperature $27^{\circ} C$ and occupy a volume of $20 L$. The gas is first expanded at constant pressure until the volume is doubled. Then it undergoes an adiabatic change until the temperature returns to its initial value.
$(1988,6 M)$
(a) Sketch the process on a $p$ - $V$ diagram.
(b) What are the final volume and pressure of the gas?
(c) What is the work done by the gas?
Show Answer
Answer:
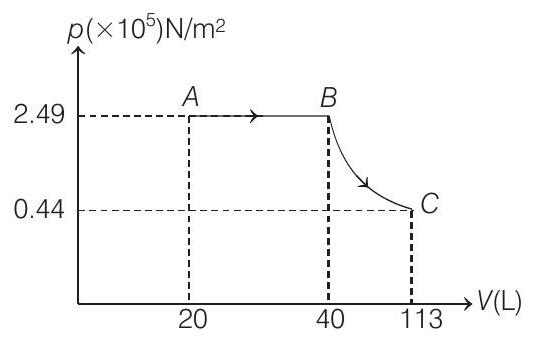
Correct Answer: 40. $(a)$
$\text { (b) } 113 \mathrm{~L}, 0.44 \times 10^5 \mathrm{~N} / \mathrm{m}^2 \text { (c) } 12459 \mathrm{~J}$
Solution:
- (a) and (b) Process $\boldsymbol{A B} p=constant$
$$ \therefore \quad V \propto T $$
i.e. if $V$ is doubled, $T$ also becomes two times.
$$ \begin{aligned} T _A=300 K & \Rightarrow \therefore T _B=600 K \\ V _A=20 L & \Rightarrow \therefore V _B=40 L \\ p _A=\frac{n R T _A}{V _A} & =\frac{(2)(8.31)(300)}{20 \times 10^{-3}} \\ & =2.49 \times 10^{5} N / m^{2} \end{aligned} $$
Process 2 Process is adiabatic. So, applying $T^{\gamma} p^{1-\gamma}=$ constant
or $\left(\frac{600}{300}\right)^{5 / 3}=\left(\frac{2.49 \times 10^{5}}{p _c}\right)^{5 / 3-1}=\left(\frac{2.49 \times 10^{5}}{p _c}\right)^{2 / 3}$
$\therefore p _c=\left(2.49 \times 10^{5}\right)\left(\frac{300}{600}\right)^{5 / 2} \Rightarrow p _c=0.44 \times 10^{5} N / m^{2}$
Similarly, using $p V^{\gamma}=$ constant we can find that $V _c=113 L$
The corresponding $p-V$ graph is shown above
(c) $W _{A B}=$ Area under $p$ - $V$ graph
$$ \begin{aligned} & =\left(2.49 \times 10^{5}\right)(40-20) \times 10^{-3}=4980 J \\ W _{B C} & =-\Delta U=n C _V\left(T _B-T _C\right) \\ & =(2)\left(\frac{3}{2} \times 8.31\right)(600-300)=7479 J \\ \therefore W _{\text {net }} & =(4980+7479) J=12459 J \end{aligned} $$






